Chapter 6 of Rudy Rucker's The Fourth Dimension: Toward a Geometry of Higher Reality is called "What We're Made Of." It's the first chapter of Part II, which he simply titles "Space."
He begins:
We are accustomed to thinking of the world as made up of lumps of matter floating in empty space. Matter is something, and space is nothing. But is this really correct? In the past, many powerful thinkers have held that the space between visible objects is filled with a subtler material, a smooth and continuous substance, a "universal plenum," or aether.
As we can see, this chapter leans more towards physics than mathematics. We usually think of aether as a pre-Einstein concept that the theory of relativity has ruled out. But according to Rucker, Einstein still incorporated aether in his theory to explain how gravity can act at a distance.
Of course, there has been much discussion about Einstein's theory in the news lately, first with the 100th anniversary of the theory and then the discovery of gravitational waves. The newly discovered waves explain how gravity acts a distance without any need for an ether. Still, we can't fault Rucker for writing about aether 30 years before the gravitational waves were discovered.
This chapter, like Chapter 3, contains six puzzles, so I can summarize this chapter much more efficiently by posting the puzzles:
Puzzle 6.1:
In Astria, Charles H. Hinton's version of Flatland, it is explicitly assumed that the two-dimensional creatures have a slight thickness, and that they are sliding around on a hard surface. They are like cold cuts lying on a flat tray of space, a space that serves as an elastic medium for transmitting all kinds of vibrations. Deep within the tissue of his or her body, each Astrian has a sharp little 3-D bump, a sort of "astral vibrator." This vibrator, about the size of a phonograph needle, oscillates with the rhythm of each Astrian's thoughts so as to set up sympathetic vibrations in the underlying space. Any other Astrian who is nearby can, without really knowing how, pick up the flavor of these thoughts from the vibrations of his own bump. What kind of impression would the Astrians get of one of their fellows who had been turned over in the third dimension?
Answer 6.1:
The turned-over Astrian would have his or her vibrator uselessly sticking up away from space. Such a person might seem to be without atmosphere or sensitivity, a zombie, a man without qualities, a burnt-out case. Is it interesting here to recall that some early thinkers, including Rene Descartes, thought that the pineal gland, located in the brain's center, might serve as a sort of third eye that perceives other people's auras or astral vibrations.
Commentary: This gives a new brand-new meaning to "I think, therefore I am"!
Puzzle 6.2:
As in puzzle 6.1, we will think about Astrians as being two-dimensional creatures who slide about on top of their space-aether. Each Astrian has a kind of higher-dimensional tooth that digs down into the firm, underlying space. How might the Astrians use meditation techniques to levitate?
Answer 6.2:
If an Astrian could dig his little 3-D thorn into underlying space hard enough, then he could oppose a force of gravity pulling him across space. In Charles H. Hinton's 1907 novel, An Episode of Flatland, this is exactly what the Astrians do....
Commentary: At this point Rucker quotes the novel written by Hinton, a contemporary of Edwin Abbott Abbott (the author of the original Flatland). I find no need to repeat the quote.
Puzzle 6.3:
We assume that Flatlanders [Abbott's original version, not Hinton's -- dw] are actually in their space, like inkblots in thin paper, or like color swirls in a soap film. A Flatlander cannot exist out of his or her space. But how, then, was A Cube able to lift A Square out of Flatland's space and turn him over [the reflections from Chapter 4 -- dw]?
Answer 6.3:
A Cube snipped the piece of space containing A Square and turned the piece over. Now you might worry about the space of Flatland "popping" from having a hole in it. Well, perhaps A Cube took care of that by using something like embroidery rings to clamp down around the edges of the hole and of the cut-out piece. Or maybe there was just a hole in space for a while. What would it be like to have a hole in space? We'll get back to the question in Chapter 7.
Puzzle 6.4:
Suppose we believe, along with Einstein, that it is possible [I believe Rucker errs here -- he means to say "impossible," so that the rest of the question makes sense -- dw] to permanently mark or label a given point in space. But now suppose that we find a hole in space. Doesn't the hole serve to single out a definite space location?
Answer 6.4:
No, for we cannot tell whether the hole is moving toward space. This is analogous to the fact that a particular matter bump does not serve to mark out some particular region of the fabric of space: as a wave moves across the water, its component water bits are constantly changing. We might compare a moving space hole to a bubble floating up through a liquid. Although the bubble's shape and size stay the same, the bits of liquid that lie at the bubble's boundary are changing as the bubble moves. An offbeat idea suggested by these considerations is that perhaps the smallest components of matter are not vortices or space bumps but actual holes in space.
Puzzle 6.5:
Quasars are very bright, very distant objects. Recently astronomers found two quasars that seem to be unusually close to each other. Further analysis of these two spots of light revealed that what we are seeing is actually two images of the same quasar. Can you find a "space bump" diagram that show how one quasar's image can be split into two?
Answer 6.5:
The idea is that the galaxy's bump is on a line directly between us and the quasar. Light from the quasar to us can travel along two alternative shortest paths: one around either side of the galaxy's big space bump. The splitting of a quasar's image was definitely observed in 1979. (See Frederic Chaffee, "The Discovery of a Gravitational Lens," Scientific American, November 1980.) The phrase "gravitational lens" is an exciting way of expressing the fact that space curvature can bend light. It is amusing to think of a vast supertelescope based on gravitational lenses millions of miles across.
Puzzle 6.6:
Generally we have represented the space curvature caused by a bit of mass as a rounded-off hump. Suppose that bits of mass were actual points. What kind of space shape would best represent such a mass point?
Answer 6.6:
A point-sized mass can be most simply represented as a sharp cusp in space. Alternatively, one might imagine this cusp to be pulled all the way out to infinity.
Commentary: Ah yes, this is the famous "delta function," which isn't really a function at all.
This is what I wrote last year about today's lesson:
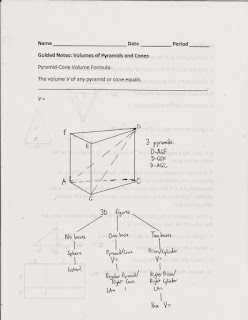
Lesson 10-7 of the U of Chicago text is on the volumes of pyramids and cones. And of course, the question on everyone's mind during this section is, where does the factor of 1/3 come from?
The U of Chicago text provides two ways to determine the factor of 1/3, and these appear in Exploration Questions 22 and 23. Notice that without the 1/3 factor, the volume formulas for pyramid and cone reduce to those of prism and cylinder, respectively -- so what we're actually saying is that the volume of a conic surface is one-third that of the corresponding cylindric surface. So Question 22 directs the students to create a cone and its corresponding cylinder and see how many conefuls of sand fill the cylinder. The hope, of course, is that the students obtain 3 as an answer. This is the technique used in Section 10.6 of the MacDougal Littell Grade 7 text that I mentioned in yesterday's post as well.
(By the way, I just realized that I mentioned four different math texts in yesterday's post! Now Rucker's book is not a math text, but it is a book -- which means that I referred to five different books in that post. And I did mention the Pappas calendar also. Even though a calendar isn't quite a book, it does mean that I mentioned six items with pages full of math in a single post! And so once again, I end up with another bloated post.)
But of course, here in High School Geometry, we expect a more rigorous derivation. In Question 23, students actually create three triangular pyramids of the same base area and height and join them to form the corresponding prism, thereby showing that each pyramid has 1/3 the prism's volume. But this only proves the volume formula for a specific case. We then use Cavalieri's Principle to show that therefore, any pyramid or cone must have volume one-third the base area times height -- just as we used Cavalieri a few weeks ago to show that the volume of any prism, not just a box, must be the base area times height.
I decided not to include either of the activities from Questions 22 or 23. After all, there was just an activity yesterday and I wish to avoid posting activities on back-to-back days unless there is a specific reason to.
In Question 11, we learn that the largest monument ever built is the Quetzalcoatl at Cholula de Rivadabia, a pyramid about 60 miles southeast of Mexico City. So in particular, the Quetzalcoatl is larger than any of the more famous Egyptian pyramids mentioned in yesterday's lesson. (But apparently, the Quetzalcoatl is well-known enough to avoid being flagged as a spelling error here on the Blogger editor.) Naturally, the students are asked to determine the volume of this large pyramid.
Question 15 invokes one of the simplest solids of revolution -- a BC Calculus staple. Of course, we only need to use the cone formula to find the volume and not anything from Calculus.
Finally, in the lesson I incorporated some of Lesson 10-6, "Remembering Formulas." I like the idea of having a section devoted solely to remembering these formulas -- since these are notoriously difficult for students to remember. The problem is that the way my lessons are set up, there is precious little time to devote an entire day's lesson just to remembering formulas. But I squeeze it in here by showing the same hierarchy of three-dimensional figures that appear in Lesson 10-6.

No comments:
Post a Comment