Lesson 15-8: The Isoperimetric Inequality (Day 138)

Today we are covering Lesson 15-8 of the U of Chicago text, on the Isoperimetric Inequality. It's a brand new lesson that I didn't cover last year. In fact, I was inspired by some of the side-along books that I've read so far this year to include this lesson.

Here are the key theorems of this lesson:

Isoperimetric Theorem:
Of all plane figures with the same perimeter, the circle has the most area.
Equivalently, of all plane figures with the same area, the circle has the least perimeter.

Isoperimetric Inequality:
If a plane figure has area A and perimeter p, then A < p^2/(4pi).

The U of Chicago text writes:

The proof of this theorem requires advanced calculus, a subject usually not studied until college. The reason the proof is so difficult is that it requires discussing all sorts of curves.

Readers of this blog should know by now that of course I'm not just going to leave it at that! I'm curious about the proof, and so I had to do some research.

Here is a link to a proof of the Isometric Inequality:

https://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/blasjo526.pdf

According to the link, the 19th century Swiss mathematician Jakob Steiner was the first to prove the Isometric Inequality -- indeed, he gave five different proofs of the theorem! And, just as the U of Chicago tells us, the proofs all involve Calculus that is well beyond AP Calculus BC.

But the link also tells us about the ancient Greek mathematician Zenodorus, who most likely lived a little after Archimedes (and thus well after Euclid). The text tells us that the full proof is so difficult because "it requires discussing all sorts of curves," but Zenodorus is able to give a simple proof of the case that a circle has a greater area than any polygon with the same perimeter.

Zenodorus's polygon proof requires demonstrating three theorems. I will provide the proofs of all three theorems as given at the link above -- with commentary, as usual.

Theorem. For regular polygons with the same perimeter, more sides implies greater area.

Proof. Consider the apothem, the radius-like perpendicular drawn from the center to a side. Half the product of the apothem by the fixed perimeter yields the area of the polygon. The apothem is the height of the triangle [one of the n congruent triangles into which a regular n-gon is divided -- dw].

If we increase the number of sides, the base of the triangle is shortened and the angle is decreased. It is clear that the height increases. We would prove this by trigonometry; Zenodorus had to rely on the usual pretrig bag of tricks. It is routine for us, and it probably was for Zenodorus as well. QED

Theorem. A circle has greater area than any regular polygon with the same perimeter.

Proof. Archimedes proved that the cut-and-roll area formula also holds for the circle. [We actually discussed this back on Pi Day. Although the formulas C = 2pi r and A = pi r^2 are difficult to derive on their own, it's easy to derive one from the other using cut-and-roll. Last year we started with area and used cut-and-roll to derive the circumference, and this year we did the opposite direction. -- dw]

So we must show that the apothem of any regular polygon is shorter than the radius of the circle with the same perimeter. Rescale the perimeter so that it circumscribes the circle [a dilation! -- dw].

The perimeter is now greater than the perimeter of the circle, and therefore greater than before the scaling. Thus the scaling was a magnification [an expansion, using U of Chicago terminology -- dw], with the apothem magnified to the size of the radius of the circle. QED

Theorem. A regular n-gon has greater area than all other n-gons with the same perimeter.

Proof: Among isoperimetric triangles with the same area, the isosceles triangle covers the greatest area. so the maximal n-gon must be equilateral. Otherwise we could improve on it by making it equilateral.

We now know that the maximal n-gon must be equilateral. Suppose that it is not equiangular [an indirect proof -- dw]. Consider two dissimilar triangles [dividing the polygon -- dw]. Now make them similar [congruent -- dw] by redistributing perimeter from the pointy to the blunt angle until the two angles are the same. This increases the area. Accordingly the maximal n-gon must be equiangular: if not, we could improve on it. QED

Combining these three proofs, we conclude that the circle has a greater area than any other polygon with the same perimeter. Now we can see why not even Zenodorus's proof isn't given in the U of Chicago text -- it depends on so many theorems (as in how fixing the perimeter of a regular polygon and increasing the number of sides must lengthen the apothem) that are difficult to prove.

The following link leads to Cut the Knot, one of my favorite websites. It gives a proof of the Isoperimetric Inequality that is essentially the first Steiner proof given at the MAA link above:

http://www.cut-the-knot.org/do_you_know/isoperimetric.shtml

Proof of Statement 1

The proof will proceed in several steps. First of all, let us note that the figure that solves Statement 1 (we hope it's a circle) must be convex. Indeed, assume it's not (see Fig 1). This would imply existence of two points from the figure such that the connecting segment would not itself lie inside our shape. Then reflecting a region between the segment and the boundary of the shape as on Fig. 2, it would be possible to increase its area without modifying its perimeter.

On the second step we proof the following

Lemma 1

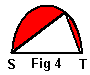
Let two points S and T be selected on the boundary of the shape solving Statement 1 such that the points divide the perimeter into two equal parts. Then the segment ST must divide the area of the shape into two equal parts.

Proof of Lemma 1

Assume, on the contrary, the area S1T is larger than T2S (Fig 3). Then reflecting S1T in ST will get the shape S1T3 with the same perimeter as S1T2 but a larger area.

From this proof it appears that it's sufficient to solve the following "half" of the problem: Among all arcs with a given length and endpoints on a line ST find the one that along with the line ST encloses the largest area. This question was previously posed elsewhere on this site.

Lemma 2

Consider all the arcs with a given length and the endpoints S and T on a fixed straight line. The curve that encloses the maximum area between the curve and the straight line is a semicircle.

Proof of Lemma 2

Suffice it to show that every angle inscribed into the arc is right. If there is a point on the arc, say P, for which ∠SPT is not right, slide either point S or point T along the straight line ST until the angle becomes right. Let pieces of the arc move along. As an exercise prove that among all triangles with two given sides the one whose sides enclose a right angle has the largest area. Since the area of the two red regions did not change but the area of the triangle (Fig 5) grew, the whole area between the new curve SPT and the line ST has increased. This shows that unless the curve is a semicircle we can always increase the area in question by moving points S and T. This proves Lemma 2 and with it Statement 1.

Elegant as it is this proof of Statement 1 contains a flaw. On each of the three steps we assumed that the shape answering conclusions of the steps existed and the Lemmas have only been proved under this assumption. Ultimately, we assumed that there exists a figure having a maximum area among all the shapes with the same perimeter. Under this assumption we proved that such a shape is bound to be a circle. Denote the existence hypothesis as H. What we have actually shown is an implication H ⇒ A. In order to prove A we still have to demonstrate that H holds true.

Existence of the optimal shape in the sense of Statement 1 is not at all obvious. For example, if Statement 1 required us to determine a shape with the smallest area for a given perimeter, such shape would not exist at all. Once we understood this point it's less important to actually complete the proof. H is proven with a limiting procedure which is quite simple but requires some basic elements of Calculus.

By the way, I'm surprised that all the figures from Cut the Knot actually copied into this post! I have a few comments to make about this proof:

-- Notice that reflections appear twice in this proof -- first in proving that the optimal shape is convex and then again in the proof of Lemma 1. In fact, we see that dilations also make an appearance -- the CTK proof that the two forms of the Isoperimetric Theorem are equivalent (Statements 1 and 2) also uses dilations. Indeed, it's a bit surprising that the U of Chicago text doesn't prove this equivalence using dilations -- instead the text solves the Isoperimetric Inequality for p. But it does show us how the Common Core transformations keep showing up in proofs.
-- The proofs of these lemmas are all indirect. ("Assume it's not" convex... "Assume, on the contrary, that the area" is larger... Assume that SPT is not a right angle....)
-- In yesterday's Lesson 15-3 we proved that an angle inscribed in a semicircle is a right angle. In this post we use the converse -- if every angle inscribed in an arc is right, then the arc is a semicircle.
-- Just like the Zenodorus proof from earlier, we have a non-obvious statement whose proof is not given: "Among all triangles with two given sides, the one whose sides enclose a right angle has the largest area." But this is easy to prove using trig -- in fact, many Geometry texts (but not the U of Chicago) give the following formula: A = ab sin(theta)/2. The area is maximum when sin(theta) = 1 -- that is, when theta = 90 degrees.
-- CTK states that this proof is incomplete because there's a statement H that has yet to be proved -- that there even exists a shape with a maximum area. It's the proof of H that requires Calculus -- otherwise we could almost include this proof in the U of Chicago text.

According to the MAA link, Steiner himself didn't bother to prove H. A later German mathematician Oskar Perron would criticize Steiner's omission by giving the following fallacious proof:

Theorem. Among all positive integers, 1 is the largest.

Proof. For any integer that is not 1, there is a method (to take the square) by which one finds a larger positive integer. Therefore 1 is the largest integer. QED?

(This "theorem" is also known as Perron's Paradox.) Here's what Perron actually proved: "either 1 is the largest integer or there is no largest integer." And of course, it's the latter statement that's true, but if Perron's proof is invalid, then so is Steiner's, unless H can be proved. It would take nearly a century after Steiner before H was finally proved.

But notice that all of these theorems can be generalized. Given a class of figures with the same perimeter, notice that the one with the largest area tends to be the most symmetrical. Cut the Knot generalizes this observation:

1. Among all triangles with the same perimeter, the equilateral one has the largest area
2. Among all quadrilaterals with the same perimeter, the square has the largest area
3. In particular, among all rectangles with the same perimeter, the square has the largest area
4. This latter fact is equivalent to √ab ≤ (a + b)/2, a particular case of the inequality between the geometric an arithmetic means.
5. ...
6. Among any finite number of regular polygons with the same perimeter, the one with the largest number of sides has the largest area.
7. Among all n-gons (n fixed) with the same perimeter the regular one has the largest area. (This is known as Zenodorus Theorem, see [Tikhomirov, pp 11-15].
8. Each of the statements above has an equivalent where the area is given.
9. As in Lemma 2, among all plane curves of fixed length with fixed endpoints, a circular arc encloses a maximum area between it and the line joining its endpoints.
10. Of all polygons with n sides inscribed in a given circle, the regular one has the largest area.

The three Zenodorus proofs help us out with the bonus question on the worksheet as well. It asks for the dimensions of a polygon with perimeter 100 feet and area greater than 625 square feet. We see that a square with perimeter 100 ft. has sides of length 25 ft. and area 625 sq. ft. -- and we know that the square has the greatest area of all quadrilaterals with perimeter 100 feet (generalization #2 from the above list). So the answer to the bonus question can't be a quadrilateral.

But we also proved that as the number of sides of a regular polygon increases, the area of the polygon increases as well (generalization #6 from the above list). So any regular polygon with more than four sides will work. For example, a regular pentagon with sides of length 20 ft. will have perimeter 100 ft. and area more than 625 square feet, and a regular decagon with sides of length 10 ft. will have an even larger area.

According to one of the review questions, "if we finish the next lesson, our class will have done every lesson in the book." Note that Lesson 15-8 is the penultimate lesson of the U of Chicago text.