It also marks four full years since my very first post here on the blog. Yes, I've declared Pi Day of the Century -- March 14th, 2015, to be the ceremonial start date of this blog. But the chronological start date was July 22nd, 2014. I like celebrating both Pi Day and Pi Approximation Day -- including eating pie both days -- and so I celebrate both of them as launch dates for the blog.
Last year, I used the anniversary to create a FAQ about my blog and myself. I do the same this year -- and this year's FAQ will reflect the changes that have happened to my career since last year. As usual, let me include a table of contents for this FAQ:
1. Who am I? Am I a math teacher?
2. Who is Theoni Pappas?
3. How did I approximate pi in my classroom?
4. What is the U of Chicago text?
5. Who is Fawn Nguyen?
6. Who are the traditionalists?
7. What's with the "line and its translation image are parallel" proof?
8. What's "Mocha music"?
9. Mocha Music for Pi Approximation Day
10. How should have I stated my most important classroom rule?
1. Who am I? Am I a math teacher?
I am David Walker. I'm trying to start a career as a math teacher, but I must admit that my career isn't off to as good a start as I'd like.
Two years ago was my first as a teacher at a charter middle school, but I left that classroom. And this summer, I was just about to start teaching a high school summer class, but I was told that summer enrollment at the school is declining, and so they decided not to hire me as a teacher.
By now, I fear that I won't be hired to teach this year at all. If I'm not hired, then I'll remain a substitute teacher. But this will make the launch of my teaching career that much more difficult.
So the answer to this question is no, I'm not currently a math teacher, but I'm hoping that I'll be one again soon.
2. Who is Theoni Pappas?
Theoni Pappas is the author of The Mathematics Calendar. In most years, Pappas produces a calendar that provides a math problem each day. The answer to each question is the date. I will post the Pappas questions for each day that I blog, provided that it's a Geometry question.
The question for July 22nd this year is Algebra, and so normally I won't post it. But for the sake of today's FAQ, I'll post the Pappas question:
If a != b/3 (ASCII for "if a does not equal b/3),
(-11/0.5)(3a - b)/(b - 3a) = ?
To solve this problem, we notice that (3a - b)/(b - 3a) is just -1. Interestingly enough, the Pappas question for two days ago (July 20th) featured a similar simplification to -1. The a != b/3 restriction is there just to make sure that the denominator isn't zero.
So now we have (-11/0.5)(-1) or 11/0.5. Dividing by 0.5 (or 1/2) is the same as multiplying by 2 -- if you don't see this, then set up the decimal long division -- dividing 0.5 into 11 is equivalent to dividing 5 into 110. Either way, we obtain 22 as the answer -- and of course, today's date is the 22nd.
Two years ago, as I was about to begin my first year of teaching, I came up with the idea of starting each class with my own Pappas question -- a Warm-Up question whose answer is the date. But this quickly fell apart when I found out that our school curriculum provided a "daily assessment" question that I was required to give as the Warm-Up. Of course, the answers to these questions weren't just the date. In hindsight, I should have used the Pappas question as an Exit Pass at the end of the class, rather than a Warm-Up at the start of class. In fact, if I ever get my own class again, I might use Pappas questions as Exit Passes.
3. How did I approximate pi in my classroom?
Since today is Pi Approximation Day, I should write something about approximating pi. I won't let my disappointment -- of thinking I'd be hired at a new job only to be denied -- get in the way of celebrating the special day.
The dominant approximation of pi in my classroom was, of course, 3.14. I didn't quite reach the unit on pi in my seventh grade class -- Grade 7 being the year that pi first appears in the current Common Core Standards. But I did reach a unit on the volume of cylinders, cones, and spheres in my eighth grade class.
The main driver of my use of 3.14 as the only approximation of pi was IXL. I used this software to review the volume problems with my eighth graders. The software requires students to use 3.14 as pi, even though I provided them with scientific calculators with a pi key. For example, the volume of a cylinder of radius and height both 2 is 8pi cubic units. IXL expects students to enter 8(3.14) = 25.12, even though 8pi rounded to the nearest hundredth is 25.13. IXL will charge the students with an incorrect answer if they enter 25.13 instead of 25.12. And even on written tests, I didn't want to confuse the students by telling to do something different for written problems, and so I only used 3.14 for pi throughout the class.
But there was another problem with our use of calculators to find volumes. Some of the calculators were in a mode to convert all decimals into fractions. Thus 25.12 appeared as 628/25 -- and I couldn't figure out how to put them in decimal mode. This actually allowed me to catch cheaters -- only one of the calculators was in mixed number mode. Here was one of the problems from that actual test, where students had to find the volume of a cylinder of radius and height both 3:
V = pi r^2 h
V = (3.14)(3)(3)(3)
V = 84 39/50
so it displayed 84 39/50 instead of 84.78 or 4239/50. So any student who wrote 84 39/50 on the test -- other than the one I knew had the mixed number calculator -- must have been cheating.
Here's an interesting question -- suppose instead of catching cheaters, my goal was to make it as easy as possible on my students as well as my support staff member, who was grading the tests. That is, let's say I want to choose radii and heights carefully so that, by using 3.14 for pi, the volume would work out to be a whole number (which appears the same on all calculators regardless of mode). How could have I gone about this?
The main approximation of pi, 3.14, converts to 314/100 = 157/50. It's fortunate that 314 is even, so that the denominator reduces to 50 rather than 100. So our goal now is to choose a radius and height so that we can cancel the 50 remaining in the denominator.
We see that 50 factors as 2 * 5^2. The volume of a cylinder is V = pi r^2 h -- and since r is squared in this equation, making it a multiple of five cancels 5^2. It only remains to make h even to cancel out the last factor of two in the denominator. Let's check to see whether this works for r = 5, h = 2:
V = pi r^2 h
V = (3.14)(5)^2(2)
V = 157 cubic units
which is a whole number, so it works.
If we had a cone rather than a cylinder, then there is a factor of 1/3 to deal with. We can resolve the extra three in the denominator by making h a multiple of six (since it's already even). Let's check that this works for r = 5, h = 6:
V = (1/3) pi r^2 h
V = (1/3)(3.14)(5)^2(6)
V = 157 cubic units
Spheres, though, are the trickiest to make come out to be a whole number. This is because spheres, with the volume formula V = (4/3) pi r^3, have only r with no h. Thus r must have all of the factors necessary to cancel the denominator. Fortunately, the sphere formula contains the factor 4/3, and the four in the numerator already takes care of the factor of two in the denominator 50. And so r only needs to carry a factor of five (only one factor is needed since r is cubed) and three (in order to take care of the denominator of 4/3). So r must be a mutliple of 15. Let's check r = 15:
V = (4/3) pi r^3
V = (4/3)(3.14)(15)^3
V = 14130 cubic units
Notice that the volume of a sphere of radius 15 is actually 14137 to the nearest cubic unit -- that's how large the error gets by using 3.14 for pi. Nonetheless, 15 is the smallest radius for which we can get a whole number as the volume by using pi = 3.14.
Now today, Pi Approximation Day, is all about the approximation 22/7 for pi. Notice that if we were to use 22/7 as pi instead of 157/50, obtaining a whole number for the volume would be easier.
For cylinders, the only factor to worry about in the denominator is seven. Either the radius or the height can carry this factor. So let's try r = 1, h = 7:
V = pi r^2 h
V = (22/7)(1^2)(7)
V = 22 cubic units
For cones, we also have the three in 1/3 to resolve. Let's be different and let the radius carry the factor of three this time. For r = 3, h = 7, we have:
V = (1/3) pi r^2 h
V = (1/3)(22/7)(3^2)(7)
V = 66 cubic units
For spheres, unfortunately our radius must carry both three (for 4/3) and seven, and so the smallest possible whole number radius is 21:
V = (4/3) pi r^3
V = (4/3)(22/7)(21)^3
V = 38808 cubic units
This is larger than the radius of 15 we used for pi = 3.14. But notice that there are many extra factors of two around in the numerator -- 4/3 has two factors and 22/7 has one. This means that we can cut our radius of 21 in half. Even though 21/2 is not a whole number, the volume is nonetheless whole:
V = (4/3) pi r^3
V = (4/3)(22/7)(21/2)^3
V = 4851 cubic units
To make it easier on the students, I could present the radius as 10.5 instead of 21/2. (Recall that the students can easily enter decimals on the calculator -- they just can't display them.) There is still some error associated with the approximation pi = 22/7, as the volume of a sphere of radius 10.5 is actually 4849 to the nearest cubic unit, not 4851. Still, 22/7 is a slightly better approximation than 157/50 is, with a much smaller denominator to boot.
With such possibilities for integer volumes, I could have made a test that is easy for my students to take and easy for the grader to grade. I avoided multiple choice on my original test since I didn't want to give decimal choices for students with calculators in fraction mode (or vice versa). With whole number answers, multiple choice becomes more feasible. Of course, the wrong choices would play to common errors (confusing radius with diameter, forgetting 1/3 for cones).
By the way, with the summer school class I almost taught still on my mind, I point out that the two summer circle constant days (Tau Day and Pi Approximation Day) can be used as alternatives to Pi Day parties for summer classes. My district divides the summer into A Session and B Session. Tau Day, on June 28th, was the second Thursday of A Session, hence it was a perfect day for a party (especially since there is no summer school on Fridays).
Today, Pi Approximation Day is on the Sunday between the second and last weeks of B Session. Just as we would if Pi Day itself were on a Sunday, a Pi Approximation Day party would have been held on the previous school day -- Thursday, July 19th. Notice that this day is itself a day to celebrate a constant -- e Approximation Day, since 19/7 = 2.714... while e = 2.718.... Indeed, if this had been an Algebra 2B class (in which exponential functions are studied), it might have been more appropriate to call it an e Approximation Day party than a Pi Approximation Day party.
Next year, Tau Day falls on Friday (remember, no summer school on Fridays) and Pi Approximation Day falls on a Monday. Thus I'm actually hoping to teach B Session next summer. Of course, the decision to teach summer school is out of my hands since it all depends on how many students enroll.
4. What is the U of Chicago text?
In 1991, the University of Chicago School Mathematics Project published a series of secondary mathematics texts. I was able to purchase both the Algebra I and Geometry texts for two dollars each at a local public library. One thing I discovered was that the U of Chicago Geometry text is based on the same transformations that appear in the Common Core Standards -- even though the U of Chicago published the text nearly two decades before the advent of the Core.
The common denominator is NCTM, the National Council of Teachers of Mathematics. This group was behind both the U of Chicago text and the Common Core Standards. Still, this means that one can satisfy most of the Common Core Standards by teaching out of the U of Chicago text.
There are newer versions of the Geometry text than the one that I own. I've read that while my old version introduces reflections in Chapter 4 and the other isometries in Chapter 6, in the new version all isometries appear in Chapter 4.
The U of Chicago text is not the only book that I mention here on the blog, not by a long shot. Many posts here refer to the Illinois State text. This is mainly because I was a math teacher, and I used the Illinois State text when teaching at my old school.
To supplement the Illinois State text (mainly when creating homework packets), I used copies of a Saxon Algebra 1/2 text and a Saxon 65 text for fifth and sixth graders.
To learn more about some of these texts, here are some links to a webpage by Cathy Duffy. Duffy's goal is to help homeschooling parents choose a textbook for their children. Here is her review of the U of Chicago text:
http://cathyduffyreviews.com/math/geometry-ucsmp.htm
and the Saxon series:
http://cathyduffyreviews.com/math/saxon-math-54-through-calculus.htm
5. Who is Fawn Nguyen?
For years, Fawn Nguyen was the only blogger I knew who was a middle school math teacher. Back when I was a middle school teacher, I enjoyed reading Nguyen's blog, but now that I've left, it's not as important for me to focus on her blog over all others.
Nonetheless, let's take a look at Nguyen's blog today. She hasn't posted in two weeks, and so the following link is to her most recent post:
http://fawnnguyen.com/st-cloud-minnesota/
Nguyen writes about her upcoming visit to her childhood home in Minnesota. In doing so, she writes about growing up as a young Vietnamese immigrant in a new country. (The move must have been tough -- she leaves Vietnam, where the climate is tropical, and goes to Minnesota, where the climate is, um, not tropical.)
Nguyen begins:
I don’t remember the landing. It’s been a very long flight. Nor do I remember walking through the airport. We have no luggage anyway, like none.
My first memory of America is sitting in the back seat of TuAnh’s uncle’s car — an Oldsmobile wagon with wood panel trim. I’m almost eleven and a half years old, and this is the second time I’m in an automobile, a car car, which is much smoother than a bus or a van, and you’re not squished between strangers. The Oldsmobile is taking us straight home, not having to make a million stops along the way like my last bus ride from Saigon to Mũi Né.
So Nguyen must have been around the sixth grade when she moved -- and now she's a sixth grade teacher.Nguyen writes:
I will sit and watch the news with the uncle. I have no idea what they are saying, but I just like seeing white people’s faces and listening to how fast they talk. The best part is there’s always something on TV, there’s no curfew. I have two favorite shows, The Price is Right and Happy Days. You don’t have to understand very much English to watch The Price because prices are numerical, and English numbers look the same as Vietnamese numbers, except Americans are weird to write $50 instead of 50$. They claim to read from left to right too.
Hey, The Price Is Right is one of my favorite game shows, too! But Nguyen's story takes place during the show's earliest seasons in the 1970's, when Bob Barker (with dark hair) was still the host. Nguyen writes that she doesn't need to know much English to understand numerical prices or math, while Common Core often requires students to explain their answers, which can be difficult for English learners like the young Nguyen.
She continues:
I like Happy Days because it’s a show with cute boys, Chachi and Fonzie. (My family calls me Fawnzie. My name morphed from Phương to Fawn to Fawnzie. More recently, my son Gabriel probably sensed that I was stressed in our conversation and said, “Mom, I need you to be Fawnzie right now.” And I knew what he meant.)
That's interesting -- so her name "Fawn" isn't really a color, but is actually the Anglicized version of her birth name Phuong.
Fawn Nguyen -- um, Phuong Nguyen -- concludes:
I get to visit St. Cloud this August; it’ll be my first time back since I left in 1979. I’ll be facilitating a full-day workshop, and St. Cloud will just be 70 miles away. I’m flushed with nostalgia and gratitude — going back to my first home in America.
I hope Fawn Nguyen posts again on her blog soon!
6. Who are the traditionalists?
I use the phrase "traditionalists" to refer to those who oppose Common Core for mathematical -- not political -- reasons. The traditionalists tend to believe that many of the topics in the Common Core Math Standards are taught too late.
My own relationship with the traditionalists is quite complex. I tend to agree with the traditionalists regarding elementary school math and disagree with them regarding high school math.
For example, they believe that the standards in Grades 4-6 that require the use of the standard algorithm for arithmetic should move down at least one grade level. I tend to agree with the traditionalists on this point here -- most of the reasons for opposing direct instruction, rote memorization, and drill don't apply to the youngest students. I remember once learning about two nonstandard algorithms for addition -- the Left-Right Method and the Plus-Minus Method -- on an old 15-minute math show for sixth graders, "Solve It," that used to air on our local PBS station back when I was that age. For mental math, these nonstandard algorithms are great, but for a young elementary student first learning to add two-digit numbers I prefer the standard algorithm.
On the other hand, the traditionalists also prefer that high school seniors take AP Calculus in order to open the door to college STEM majors. In particular, some STEM colleges here in Southern California, such as Cal Tech and Harvey Mudd, require calculus for admission. Even colleges that don't formally require calculus are likely to send students rejection letters if they apply without having calculus on the schedule, especially if they apply to STEM majors. Therefore they want the classes leading up to senior year to prepare students to take AP Calculus -- including Algebra I in the eighth grade. They oppose Common Core because its eighth grade math standards do not comprise a full Algebra I class. I only partially agree because I don't want seniors who can't handle AP Calculus or eighth graders who can't handle Algebra I to be labeled failures. Just as AP Calculus can open the door to STEM, it can close the door to a non-STEM career if students are forced to spend too much effort trying to pass their high school math classes.
OK, so I support the traditional pedagogy with regards to elementary math and oppose it with regards to high school math. But what's my opinion regarding traditionalism in middle school math -- you know, the grades that I'll actually be teaching? In middle school, I actually prefer a blend between the traditional and progressive philosophies. And the part of traditionalism that I agree with in middle school is making sure that the students do have the basic skills in arithmetic -- since, after all, that is elementary school math, and with elementary math I prefer traditionalism.
I've referred to many specific traditionalists during my four years of posting on the blog. The traditionalist who is currently the most active is Barry Garelick. Here is a link to his most recent post:
https://traditionalmath.wordpress.com/2018/07/20/levels-of-understanding/
Garelick teaches middle school math right here in California. One of his frequent commenters is SteveH, a traditionalist in his own right. I consider SteveH to be a co-author of Garelick's blog since he posts there so often.
Let's look at Garelick's post in more detail:
There are different levels of understanding. While there are some concepts that a student may not understand, there are still connections that students make to previously learned material and concepts which serve to inform a recently learned procedure—and ultimately may lead to further understanding. In freshman calculus, for example, students learn an intuitive definition of limits and continuity which then allows them to learn the powerful applications of same; i.e. taking derivatives and finding integrals. It isn’t until they take more advanced courses (e.g., real analysis) that they learn the formal definition of limits and continuity and accompanying theorems. Does this mean that they don’t understand calculus?
As Garelick explains, the problem is with basic math, such as the times tables. Traditionalists want students to reach the point where students can answer a one-digit multiplication problem in one second, so that they can move on and use multiplication to solve harder problem. But opponents of the traditionalists -- in this post, Garelick calls them reformers (including proponents of the Common Core) -- insist that students should have a deeper "understanding" of multiplication. To the reformers, the ability to multiply single digits in one second shows only that a student is a "math zombie" -- someone who can give the correct answer without truly understanding why it is correct.
Garelick concludes:
The reform movement has succeeded in foisting its beliefs upon ever growing populations of new teachers who believe this is the only way. It is so entrenched, that even teachers who adamantly oppose such views feel guilty when teaching in the traditional manner so reviled by well-intentioned reformers. Given that today’s employers are complaining over the lack of basic math skills their recent college graduate employees possess, the math reform movement has created a poster child in which “understanding” foundational math is often not even “doing” math.
That line about "lack of basic math skills" explains why Garelick disagrees with the reformers. The reformers are so concerned that the students "understand" multiplication that in the end, they aren't able to do any actual multiplication at all.
Garelick provides an example of a traditional problem that, to him, also exhibits understanding:
One proxy that teachers use for understanding and transfer of knowledge, is how well students can do all sorts of problem variations. A student in my seventh grade math class recently provided an example of this. As an intro to a lesson on complex fractions, I announced that at the end of the lesson they would be able to do the following problem:
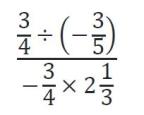
The boy raised his hand and said “Oh, I know how to solve that.” I recognized this as a “teaching moment” and said “OK, go for it”. He narrated what needed to be done: “You divide the two fractions on top, by flipping the second one and multiplying, and since one is negative you’ll get a negative answer. You get -5/4. Then you do the bottom, and you have to convert to a fraction by multiplying 2 by 3 and adding 1, so you get 7/3 , and you multiply and you cross cancel and get -7/4 .” Now you divide by -7/4 so you flip the -7/4 and multiply. You have two negatives so your answer is positive. And you can cross cancel. You get 5/7.”
One commenter, SteveH, responds to this problem:SteveH:
Your complex fraction problem does require a whole lot of mathematical understanding to solve correctly. Even if students could (properly) prove why “invert and multiply” works, they would still need a lot more understanding to solve the problem. What if you had ((-3)/5)) in the numerator or (3/(-5)). There is never any reason to prove everything before you use it or understand it at a deep level. Also, understanding a proof does not give one the flexibility of understanding achieved from doing lots of P-sets. Astoundingly, one of the core ideas for many in education is the belief that understanding (conceptual or whatever) allows for less individual homework. In K-6, they claim hegemony over content, skills, and understanding even though their only academic turf is education (process). However, they then do little as a guide on the side. Student, teach thyself!
"Guide on the side" is a reform-minded teacher. A traditionalist teacher is a "sage on the stage."
By the way, SteveH and other traditionalists criticize the need to "explain everything." To this extent, someone like Fawn Nguyen would agree (recall her statements about being a young English learner and not needing to know English to understand numerical prices). On the other hand, Nguyen and SteveH strongly disagree on homework -- Nguyen doesn't believe in grading HW or assigning a lot of it, while to SteveH, HW (in the form of "P-sets" or problem sets) are crucial.
But the commenter I want to focus on today is Wayne Bishop:
Wayne Bishop:
A friend who, for years, worked with ETS on the CSU-wide ELM (Entry Level Mathematics exam, now defunct) observed that a single item on the exam correlated so well with passing the exam and subsequent success in the student’s choice of non-remedial college math that the rest of the test could be ignored. What was it? Simplification of a modestly complicated complex rational function (algebra fraction). Without verbalizing anything, recalling the arithmetic properties of fractions along with the (always arranged to be trivial) factoring well enough to complete the task correctly is enough for a reasonable promise of mathematics success at any CSU campus. Now we use the SBAC (Smarter Balanced Assessment Consortium of Common Core) exam for admission math competence. No such item.
A while ago, someone (clearly not a traditionalist) criticized the appearance of rational expressions on the CSU (California State University) math test. (As so often happens, I read a website and don't immediately blog about it -- then when I do want to blog about it, I can't find the link!) Anyway, whoever this person was wrote that rational expressions are useless in real life, yet their appearance on the ELM was torture and blocked bright students from obtaining college degrees.It could have been the following 2015 post from the famous math blogger Dan Meyer, except that this link doesn't specifically mention the ELM:
http://blog.mrmeyer.com/2015/if-simplifying-rational-expressions-is-aspirin-then-how-do-you-create-the-headache/
Anyway, Bishop's post implies that not only should rational expressions appear on the test, but they should be the only questions on the test! Rational expressions might be useless in real life, but their presence on the test guarantees that only smart students -- those who are likely to get A's in classes such as Calculus and above -- are admitted to STEM majors.
Even though I didn't end up teaching summer school, I was given access to the Edgenuity software that these classes use -- including classes that I was never expected to teach, such as Algebra 2B. I can report that on the "Rational Functions" quiz, one girl earned a perfect score, while three students earned 88 on the test (high B/B+). On the flip side, one student failed with a 52, while another student scored 60 (low D/D-). Following Bishop, this quiz should be the ELM. Instead, the ELM has been replaced with a Common Core test that doesn't emphasize rational expressions -- much to the delight of the blogger who compared them to torture.
7. What's with the "line and its translation image are parallel" proof?
Both this year and in past summers, I devoted several posts out of the blue to the proof of a statement from Geometry, "a line and its translation image are parallel." The reason for this proof goes back to the goals of Common Core Math and the traditionalist debate.
Let's go back to the comment made earlier by the traditionalist SteveH:
SteveH:
There is never any reason to prove everything before you use it or understand it at a deep level. Also, understanding a proof does not give one the flexibility of understanding achieved from doing lots of P-sets.
Here SteveH was discussing the proof of basic multiplication of integers, or perhaps the rule for division of rational numbers. I agree that "proofs" of these statements are unnecessary. But there's one math class where proofs are expected even in traditionalist classes -- Geometry.
But the Common Core takes Geometry proofs a step further. The Common Core expects students to prove statements that traditionalists take for granted, such as the triangle congruence properties (that is, SSS, SAS, and ASA.) These statements are proved using transformations -- reflections, rotations, and translations.
Now it's possible to take this a step further. The parallel line properties (that is, Corresponding Angles and its converse) can also be proved using transformations. One of the first mathematicians to do so is UC Berkeley professor Hung-Hsi Wu. The two things to note about his proof are:
- Wu uses 180-degree rotations to map one parallel line to another. Therefore, his main proof is for the Alternate Interior Angles Test rather than Corresponding Angles.
- Wu delays using a parallel postulate as late as possible. In particular, he is able to prove the Alternate Interior Angles Test (that is, if ... then the lines are parallel) without any need for a parallel postulate at all. So his proof is valid in both Euclidean and hyperbolic geometry. On the other hand, the converse requires a parallel postulate (Playfair's).
Using Wu's proof, we can avoid the parallel postulate until a certain point when it's needed. Then later on, we can mention that there's another type of geometry called hyperbolic geometry -- and that all the proofs so far are valid in hyperbolic geometry up to the point where Wu first invokes Playfair.
Unfortunately, I find two problem with this approach:
- Wu's proof depends on 180-degree rotations, but for most students, translations are easier to understand than rotations. I once saw a website (now defunct) that demonstrated translating one parallel line to another to show that corresponding angles are congruent. It would be nice if I could convert that animation into a rigorous proof.
- Wu's proof is valid in hyperbolic geometry, but who cares, since we usually don't discuss hyperbolic geometry in high school math anyway. If we're going to mention non-Euclidean geometry at all, it would be spherical geometry -- after all, we live on a sphere. Some honors classes even introduce spherical geometry at the end of the year. It would be nice if I had a proof that, if valid in a second geometry at all, is valid in spherical, not hyperbolic, geometry.
On July 12th, I finally posted a valid proof of the Corresponding Angles Consequence. But this proof turns out to be very complicated. For example, I used the following theorem:
Three Perpendiculars Theorem:
If three lines are perpendicular to the same line, then the three lines are either parallel or concurrent.
This theorem is valid in both Euclidean and spherical geometry -- in particular, the "parallel" part is Euclidean, while the "concurrent" part is spherical.
But Three Perpendiculars isn't the sort of theorem we want to teach in high school. And besides, we're trying to prove something about parallel lines, and there are no parallels on the sphere. Thus it's silly to prove these theorems in both Euclidean and spherical geometry, even if technically they're valid (for example, "if two parallel lines are cut by a transversal" is vacuously true on the sphere).
I completed the proof only because I wanted to finish what I started. But my final result is definitely inappropriate for a high school class. Perhaps instead of working on both goals, it might be better to focus on one or the other:
- We might replace Wu's 180-degree rotations with translations to prove statements that are valid and meaningful in both Euclidean and hyperbolic geometry. At the end of the year, we might say that there's a geometry called hyperbolic -- show the students the Numberphile video.
- We might mention spherical geometry at the end of the year, but only in connection to statements that are true in both Euclidean and spherical geometry (such as SSS, SAS, ASA), not parallel lines.
I won't pursue this any further. On the blog, my lessons are based on the U of Chicago text, where both Corresponding Angles and its converse are postulates.
If I ever teach in a classroom again, then it depends on the grade level. In eighth grade, where transformations are introduced but no formal proofs are given, we can informally show them that we can translate corresponding angles to each other -- as well as map alternating interior angles to each other via a 180-degree rotation. That way, the eighth graders can learn that these pairs of angles are congruent without having to teach them vocabulary -- "corresponding" or "alternate interior" angles.
In a Geometry class, it all depends on what text is being used. If parallel line postulates appear transformations, then I could show them how transformations can be used to prove the parallel line statements without delving too deeply with "Three Perpendiculars" or other nonsense. If parallel lines appear before transformations (as they do in the U of Chicago text) then just forget about it.
By the way, the statement I was trying to prove -- "a line and its translation image are parallel" -- doesn't even appear in the Common Core Standards. On the other hand, "a line and its dilation image are parallel" does explicitly appear in the standards. So this is something that we can keep in mind -- but then again, parallel lines usually appear well before dilations in most texts, so it's not as if we could use dilations to prove the parallel line statements.
8. What's "Mocha music"?
In many recent posts, I refer to something called "Mocha music." This is a good time to explain what Mocha music actually means.
When I was a young child in the 1980's, I had a computer that I could program in BASIC. This old computer had a SOUND command that could play 255 different tones. But these 255 tones don't correspond to the 88 keys of a piano. For years, it was a mystery as to how SOUND could be used to make music. Another command, PLAY, is used to make music instead, since PLAY's notes actually do correspond to piano keys.
Last year, I found an emulator for my old BASIC computer, called Mocha:
When we click on the "Sound" box on the left side of the screen, Mocha can play sounds, including those generated by the SOUND command. So finally, I could solve the SOUND mystery and figure out how the Sounds correspond to computer notes.
I discovered that SOUND is based on something called EDL, equal divisions of length. We can imagine that we have strings of different lengths -- as in a string instrument or inside a piano. The ratio of the lengths determine their sound -- for example, if two strings are in a 2/1 ratio, then the longer string sounds an octave lower than the shorter string.
The key number for SOUND is 261, the "Bridge" (or end of the string). Mocha labels the Sounds from 1 (low) to 255, so we subtract these numbers from 261 to get a Degree ranging from 260 (long string) to 6 (short string). The ratios between the Degrees determine the intervals. I found out that the Degrees corresponding to powers of 2 (8, 16, 32, 64, 128, 256) sound as E's on a piano, with Degree 128 being the E just above middle C (that is, E4).
Let's say we were to play the following two notes on Mocha:
10 SOUND 51,8
20 SOUND 86,8
The second number 8 indicates a half note, since 8 is half of 16 (the whole note). But we want to focus on the first numbers here, which indicate the pitches (tones).
We first convert the Sounds to Degrees. Since 261 - 51 = 210, the first note is Degree 210. The Degree of the second note is 261 - 86 = 175. Now the ratio between these two Degrees is 210/175, which reduces to 6/5. This is the interval of a minor third, so the two notes are a minor third apart. As it turns out, the two notes sounds as G and Bb -- "greenish G" and "greenish-green Bb."
Let's try another example:
30 SOUND 144,8
40 SOUND 196,8
Warning -- we don't attempt to find the ratio 196/144 (which is 49/36 by the way). We only find the ratios of Degrees, not Sounds. The Degrees are 261 - 144 = 117 and 261 - 196 = 65. Thus the interval between the notes is 117/65 = 9/5, a minor seventh. (Using Degrees instead of sounds makes a big difference, since 49/36 would be an acute fourth or tritone, not a minor seventh.) The names of the two notes played by Mocha are "ocher F" and "ocher-green Eb."
Where do all these strange color names like "green" and "ocher" come from? Actually, they refer to Kite's color notation, and the colors tell us which primes appear in the Degree:
- white: primes 2 or 3 only
- green: prime 5
- red: prime 7
- amber: prime 11
- ocher: prime 13
- umber: prime 17
- khaki: prime 19
Kite's color notation also uses colors such as yellow, blue, and so on. But these are "otonal" colors, while EDL scales/lengths of string are based on "utonal" colors only.
The website where Kite explains his color notation is set to disappear at the end of July. Actually, here's another link where Kite's color notation is explained:
Oops, I just stumbled upon this today when I was trying to find a link that isn't about to disappear at the end of July. Apparently, "Kite" (or "Tall Kite") is considering changing up the colors. So you might want to forget everything I said about colors until this debate is resolved.
9. Mocha Music for Pi Approximation Day
I keep saying that I should use these exotic Mocha scales for composing new music, not simply converting music in our usual scale (12EDO) to the new scales.
But on holidays, I'm in the mood for converting old music to the new scales. For Pi Approximation Day, I was hoping to convert songs about pi -- specifically songs that used to be posted on other websites that are now defunct. This includes "American Pi" and "Digit Connection" from the old Bizzie Lizzie Sailor Pi site, as well as Danica McKellar's old pi song based on "Dance of the Sugar Plum Fairy."
I would convert these songs if I had access to the sheet music, which I don't. Maybe I'll convert them some day, but until then, it's easier just to find YouTube videos of the songs on which these are parodies ("American Pie," etc.) and sing the pi lyrics loud enough to drown out the real words.
So instead, let's just code a pi song based on 16EDL, similar to the song we played for Tau Day:
NEW
10 N=16
20 FOR X=1 TO 32
30 READ A
40 SOUND 261-N*(17-A),4
50 NEXT X
60 DATA 3,1,4,1,5,9,2,6,5,3
70 DATA 5,8,9,7,9,3,2,3,8,4
80 DATA 6,2,6,4,3,3,8,3,2,7
90 DATA 9,5
10 N=16
20 FOR X=1 TO 32
30 READ A
40 SOUND 261-N*(17-A),4
50 NEXT X
60 DATA 3,1,4,1,5,9,2,6,5,3
70 DATA 5,8,9,7,9,3,2,3,8,4
80 DATA 6,2,6,4,3,3,8,3,2,7
90 DATA 9,5
As is traditional, I stop just before the first zero. Then digits 1-9 map to Degrees 16 down to 8, with the lowest note played on E (line 10, N=16). We can change the value of N to any value from 1 to 16 to change the key.
Here's an actual song converted to 12EDL, the simplest EDL scale, the Sailor Pi theme song:
NEW
10 N=13
20 FOR X=1 TO 26
30 READ D,T
40 SOUND 261-N*D,T
50 NEXT X
60 DATA 8,4,8,2,9,4,9,2,10,4,11,4,9,12
70 DATA 9,4,9,2,10,4,10,2,11,4,12,4,10,12
80 DATA 12,4,12,2,10,4,10,2,8,4,6,4,7,12
90 DATA 8,4,9,4,10,2,11,6,12,16
Only the main verse is coded here. The "bridge" part -- which is instrumental in both the original Sailor Moon and Lizzie's Sailor Pi song -- is too hard for me to code without sheet music.
Here are the lyrics for the first verse -- the part which we coded above:
Fighting fractions by moonlight
Perplexing people by daylight
Reading Shakespeare at midnight
She is the one named Sailor Pi.
10. How should have I stated my most important classroom rule?
This is what I wrote two years ago:
Rule #3: Respect yourself and others.
Students respect themselves and each other as well as me, the teacher, by following all rules and allowing others to learn the material.
This rule worked for Fawn Nguyen, the teacher from whom I got this rule. But it didn't work in my classroom at all. Of course, a student playing with a phone case isn't respecting the teacher, but I needed a rule that would require the student to put the case away immediately.
Here's a much better rule:
Rule #1: Follow all adult directions.
And so if I say, "Put the phone case away," the student couldn't counter that phone cases were against the rules, because my direction was to put the case away.
If I ever find myself in the classroom again, this will definitely be my first and most important rule.
This is what I wrote two years ago:
Rule #3: Respect yourself and others.
Students respect themselves and each other as well as me, the teacher, by following all rules and allowing others to learn the material.
This rule worked for Fawn Nguyen, the teacher from whom I got this rule. But it didn't work in my classroom at all. Of course, a student playing with a phone case isn't respecting the teacher, but I needed a rule that would require the student to put the case away immediately.
Here's a much better rule:
Rule #1: Follow all adult directions.
And so if I say, "Put the phone case away," the student couldn't counter that phone cases were against the rules, because my direction was to put the case away.
If I ever find myself in the classroom again, this will definitely be my first and most important rule.
OK, here are some Pi Approximation Day video links:
1. Draw Curiosity
Notice that this video, from two years ago, actually acknowledges Pi Approximation Day.
2. Math Babbler:
The Math Babbler tends to post a video for Pi Approximation Day every year. In this one, he discusses how accurate the approximation 22/7 actually is.
3. Converge to Diverge
In this brand-new video from today, the speaker attempts to approximate pi just as Archimedes did it -- using a regular 96-gon.
4. Numberphile
No Pi (Approximation) Day is complete without a Numberphile video. In this video, we learn that pi is not just irrational, but is also transcendental -- that is, there doesn't even exist a polynomial f, with integer or rational coefficients, such that f (pi) = 0 (unlike sqrt(2), which is algebraic). This is even stronger than Legendre's result that pi^2 is irrational.
5. Sharon Serano
Well, I already gave ten facts about pi, and so this video is twice as good.
6. Vi Hart
No, I can't avoid another one of my favorite math YouTube posters, Vi Hart. Of course, in this video she argues that there's nothing special about pi at all
7. TheOdd1sOut
This video is specifically listed as a "Vi Hart rebuttal" to videos such as the previous video.
8. A Song Scout
This is another pi song based on its digits. Unlike Michael Blake's song (listed below), it is in the key of A minor rather than C major.
9. Michael Blake
I like the idea of using music to teach math, so here's a favorite, Michael Blake's "What Pi Sounds Like." I tried to find a way to incorporate songs such as this one into the classroom.
10. tiradorfranco2
I'm surprised that I don't post this Square One TV video on Pi Approximation Day. The song is about the mathematician who first discovered that pi is approximately 22/7 -- Archimedes. The singer even mentions how Archimedes was "busy calculating pi" at around the 2-minute mark.
Bonus: Charlie Lindelof
This video has nothing to do with Pi Approximation Day. But while I was searching for pi videos I stumbled upon the above video. It goes back to what I was saying about the traditionalist Wayne Bishop and college placement exams. This is all about a rational expression question on the Accuplacer. It appears that some California community colleges still use the Accuplacer as a math placement exam, even if the Cal States are using the SBAC instead.
Bonus: Numberphile
Earlier I wrote that Numberphile created some hyperbolic geometry videos. Here's one of the more interesting videos, about sports in hyperbolic space. This is just in case we decide we'd rather show our students hyperbolic than spherical geometry.
And so I wish everyone a Happy Pi Approximation Day.
No comments:
Post a Comment