Epiphany Post: Resolutions and the Story of a Special Scholar

Table of Contents

1. Pappas Question of the Day
2. An Epiphany About a Special Scholar

3. August-September 2016

4. October 2016

5. November-December 2016

6. January-February 2017

7. David's Lunar Calendar
8. New Year, Same Old Traditionalists
9. 2019 is an Odd Number to Fawn Nguyen

10. Conclusion: New Mersenne Prime and Phi Day

Pappas Question of the Day

Today on her Mathematics Calendar 2019, Theoni Pappas writes:

x^2 + 12x = -y^2 + 12y - 36

At what y-coordinate does the above circle intersect the y-axis?

This is my first post of the year and the first problem on the new Pappas calendar. I wasn't sure whether to post this question, though. On one hand, we know that equations of circles appear in the Common Core Geometry standards

But on the other hand, the solution to this problem is pure Algebra. The question is asking for the y-intercept of this equation -- and finding the y-intercept of a circle is no different from finding that of a line in standard form. We simply let x = 0:

0 = -y^2 + 12y - 36

y^2 - 12y + 36 = 0

(y - 6)^2 = 0

y - 6 = 0

y = 6

Therefore the lone y-intercept of this circle is 6 -- and of course, today's date is the sixth.

An Epiphany About a Special Scholar

Today, January 6th, is also known as Epiphany. It marks the end of the Twelve Days of Christmas and is celebrated in various cultures in different ways. For example, many of my seventh graders from two years ago might be celebrating Dia de Reyes, or Three Kings' Day (as in the Three Magi).

Last year, I wrote a lengthy post about my management problems from the previous year at the old charter school. In that post I wrote about my seven declared New Year's Resolutions and discussed the seven months I spent in the classroom, including one huge mistake I made each month. As it turns out, these seven errors correspond roughly to the seven resolutions -- each resolution fixes a huge mistake.

I repeat this post because I'm renewing these resolutions for the new year. I want to continue focusing on these resolutions, especially as I continue as a substitute teacher this year. Just like last year, on certain days this year I'll write "A Day in the Life" -- a summary of how applied the resolutions (often focusing on one in particular) to my subbing that day.

This also means that I'm repeating the Kwanzaa and Epiphany posts from last winter. I find these two posts important when thinking back to the old charter school. Kwanzaa is an African-American holiday while Dia de Reyes is celebrated by Latinos. These are the two major racial groups served by my old charter school, and I mention students from these groups in both posts.

Last year, I wrote that there's one student I want to write about in particular. Even though I'm not proud of my interactions with several students, there's this one girl I definitely wish to reflect upon in more detail. Indeed, my interactions with her represent everything that was wrong with my style of management.

She was an eighth grader with special needs. As I mentioned before, she wouldn't want me to go into the specific details here on a public blog, so I won't. And it goes without saying that I won't post her name on the blog.

So how should I refer to her in the post? Instead of "the special ed student," let me say "the special student" since she really was special. Or better yet, let's call her "the special scholar," since our old school regularly referred to students as scholars.

I am updating one of the resolutions this year, though -- the third resolution. I'm also cutting out large parts of this story, since it's so long and I want to squeeze other topics into this lengthy post. You may refer to last year's Epiphany post for the full story.

This post gets the "traditionalists" label, since I mention traditionalists a few times in this post.

August-September 2016

When the school year started, I wasn't sure what to do about the seating chart. I knew that if I tried to assign seats, the middle school students would have just disobeyed me and sat next to their own friends instead. This was bad when I was still trying to learn the students' names! So instead, I decided to open the year by letting the students choose which group of four desks to join. That way, they were more likely to be compliant until I learned their names. Then once I knew their names, I could change their seats to separate friends who talked too much.

Indeed, there was a flaw in this plan when it came to my 13 eighth graders. There were five boys and eight girls in the class. And of those eight girls, five formed a group of friends -- I supposed they'd be best described as a clique. (The girl who would celebrate Kwanzaa was also a member of this eighth grade clique.) So we immediately see the problem -- I was dividing the class into groups of four, yet this was a group of five girls. One girl had to be left out, and that one turned out to be -- you guessed it! -- the special scholar.

(By the way, this also caused a problem in sixth and seventh grades when dividing the class into groups for Illinois State STEM projects. I'd need to divide into groups of two or three for a project, so I asked the students to divide in order to avoid arguments. But then arguments would occur anyway as four students would try to form one group, while another student is isolated because he or she doesn't get along with any of the four. The problem is that letting the students form friendship groups is that they're rarely all of the correct size.)

In my "Day in the Life" posts, I often write about the special scholar. But as I look back at those old posts, it's often hard for me to determine which student is the special scholar because I was trying hard to conceal the kids' identities. From my August 16th, 2016 post:

11:25 -- My eighth grade class arrives. This is my smallest class, with only 12 students -- but there are only eight students present at the start of class. I begin the class the same way I start all my classes, with a Warm-Up question:

What is 2 * 2 * 2 * 2? (That is, 2 times 2 times 2 times 2.)

Most students answer correctly, although a few tried to add. A student or two is upset that the very first thing we do on the first day of school is multiply. I point out that the answer is 16 -- and that today is the 16th. I always go around to stamp correct papers -- many teachers point out that students enjoy getting stamps, and my students are no exception.

11:35 -- My student support aide arrives -- the English teacher and I are each assigned one. Actually, she arrives with the four missing students, all girls.

First of all, I believe that all four girls who arrived late were clique girls, and that the special scholar was one of them. Apparently, one clique girl arrived on time, but I doubt that she was the special scholar, for then she wouldn't have been isolated (as three others would have joined her).

And that's the second management mistake I made that day -- I told her to sit with the three girls she didn't like, and she sat alone instead, and I just let her sit there. That's another bad message I sent -- if students don't want to follow directions, they can just refuse to obey without any consequences. I should have, at the very least, compromised and told her that she had to sit with the other three girls only for the one activity that required groups of four (Dan Meyer's Personality Coordinates) and that she could sit by herself as soon as that activity was complete. This would have been better than just letting her disobey me. After all, over the course of the year I would ask her to perform hundreds -- if not thousands -- of tasks that she doesn't want to complete. And yet she would be expects to perform all of those tasks.

Now that we've identified the 2 * 2 * 2 * 2 complainer as the special scholar, let's look back at the rest of the August 16th, 2016 post to see how she reacted the rest of the period:

By the way. some students believe that they have a solution to the Konigsberg problem, but actually they are crossing one of the bridges twice (they start on island D, cross the bridge towards C, but then head back to D). I start to explain about Euler and why the problem is impossible -- and as I do so, the student who earlier complained about 2 * 2 * 2 * 2 figures out that the impossibility has to do with there being an odd number of bridges from each land! I'm impressed!

Along the way, I explain that a "dren" is a reverse-nerd -- a nerd is someone who's good at math, and a "dren" is someone who doesn't understand the basics of arithmetic. As it turns out, the student who complained about 2 * 2 * 2 * 2 enjoys this song and looks forward to my next song.

So as we see, the special scholar does some special things during the remainder of the class! Despite our initial stumble, maybe our interactions started off on the right foot after all.

My next "Day in the Life" post was my monthly post -- August 18th, 2016, the third day of school. I didn't write about the special scholar in that post -- the only eighth grade girls I mentioned (playing with a stamp pad) were non-clique girls, and the special scholar was not involved.

Oh, and as for the song I sang that day -- Square One TV's "Count on It" -- I remember that the special scholar liked this song very much, even more than "The Dren Song."

The following week, I did get into a few arguments with the special scholar. Sometimes she would try to sit with the rest of her clique by pulling up a fifth chair. When I wouldn't let her, she would at least move to an empty seat on days when one of the other four clique girls was absent. (Again, the idea --that letting the students choose the seating chart would avoid disobedience -- was flawed because it didn't account for their being five friends with groups of four.) But I didn't want any students moving during Benchmark Testing Week.

As I reflect upon my interactions, I wonder what I could have done to improve them. And this leads to my first New Year's Resolution for 2019:

1. Implement a classroom management system based on how students actually think.

This goes back to the original New Year's Resolution for 2016 that, of course, I'd long forgotten by the time August came around. Mathematician Dave Kung recommended that his viewers avoid paradoxical thinking, yet my classroom management was based on paradoxes.

I didn't force the special scholar sit next to the other three girls because I didn't want her to think that I was mean. Instead, she realized that she didn't have to obey my instructions, and so from that point on she seldom followed my directions. As you'll see later in this post, I would end up doing meanER things to her to make her play.

Thus if I'm to become the ideal classroom manager, I must know that my goal is get the students to stop saying that I'm mean or unfair -- not to get them to stop thinking it. If the students say that a punishment is unfair, punish them anyway. After the first ten times or so that I punish various students, they'll probably stop saying that I'm unfair. They'll follow my instructions grudgingly -- but they'll follow them nonetheless.

Let's return to the first day of school and how I treated the special scholar. On that day, I posted that perhaps I should have reversed the order of the activities. Here is the revised order:

1. Warm-Up: If you don't know the answer....

2. Personality Coordinates

3. Music Break

4. Bridges of Konigsberg

5. Exit Pass: What is 2 * 2 * 2 * 2?

Again, I wrote this because the Pappas-like Warm-Up questions would soon be blocked by the Illinois State Daily Assessment Questions. Thus I should have established the Pappas questions as the Exit Pass, not the Warm-Up. And I believe this order would have helped the special scholar.

When the special scholar finally sits down with the group, I should then praise her for following my instruction despite her opposition to sitting there -- and then ask her to tell me her name. This is how I should learn their names -- giving an direction and then praising for following it.

I shouldn't have needed the Benchmark Tests to know that the special scholar was one of the lower students -- her reaction to 2 * 2 * 2 * 2 should have been sufficient. I should have known that this student would need extra help -- and started thinking about how to provide it to her.

The only thing was to make sure that she didn't cheat -- it would be so easy for her to copy the answer from the neutral girl, who of course would have the correct answer. It would be better for me to sit down with her and work on the problem together -- and since there was only one other student in her cluster of four, there'd be a place for me to sit. We'd work together, and if she contributed sufficiently to the problem, I'd give her the reward.

Finally, as I wrote in previous posts, I need to separate bad academics from bad behavior. When she failed to answer 2 * 2 * 2 * 2, this was a case of bad academics -- she needed help, not punishment. I remember one day when I was telling her about how not to be a dren and she asked, "Will you be able to help me then?" I should have responded with a resounding "Yes!" Maybe then she would have understood why her seat had to be isolated -- so that it would be easier for me to help her. And of course the neutral girl was there to assist the special scholar as well.

This is how I show the special scholar that I don't want to be mean to her. This is thinking outside the box -- but first there must be a "box," the basic set of rules to be followed. And I establish this via the first New Year's Resolution:

1. Implement a classroom management system based on how students actually think.

After lunch was computer practice on IXL. The eighth graders were scheduled to have IXL on Mondays and Thursdays, while the sixth graders had it on Tuesdays and Fridays. Notice that the seventh graders didn't have IXL, while no one had it on Common Planning Wednesdays.

Let me take the time to describe how IXL works. (I hinted at this in my last post, but let me write it out now.) Students select a grade-level standard that would be assigned a letter and a number. Here are some of the eighth grade standards:

I.1 Find the constant of proportionality from a table

K.8 Multi-step problems with percents

DD.5 Quartiles

Let's say that I assigned my students Standard I.1. The computer then begins each student with a score of zero. Correct answers gain points for the students, and wrong answers lose points. Just like the SBAC, the practice is computer-adaptive, so higher scores lead to more difficult questions. The student is considered to attain mastery by reaching a score of 100.

According to this pattern, a student must answer at least 28 questions to reach a score of 100. Here is the running score if all 28 questions are answered correctly:

10-19-28-36-43-49-55-60-64-68-72-75-78-81-83-85-87-89-91-92-93-94-95-96-97-98-99-100

I'm not quite sure how many points are deducted for wrong answers. I think the intention is for the deduction to be one point from a current score of 1-10, two points from a current score of 11-20, three points from a current score of 21-30, and so on. But I don't think that the deduction in the Challenge Zone is actually a full ten points, but something like eight or nine points.

In previous posts (under the traditionalists label), I've mentioned how the SBAC fails to take full advantage of his computer adaptability.

[2019 update: I cut this part out, since it has nothing to do with New Year's Resolutions.]

But here's the thing about IXL -- I didn't grade it. So in reality, there was no incentive for the students to answer any questions at all!

But the neutral girl struggled a little with Algebra I. After all, IXL doesn't actually teach math, but only reviews it. I'd have to teach her the algebra on the side -- and I was usually too busy. Instead, the girl usually stuck to Common Core 8 questions, albeit on more advanced standards than what the rest of the students were doing.

Now some students were less interested in working on IXL. And you can probably figure out who one of those students was -- the special scholar.

For the special scholar, IXL was a struggle. Sometimes she would make it to the 20's or 30's, and then keep on getting wrong answers. Even though the clique was mostly separate, the special girl was now seated with the clique leader, who was smart but lazy. Sometimes the leader would cheat for the special girl and answer the questions for her. Other times both girls would move seats and meet with a third clique member, who would then answer the questions for both of them.

I should have implemented an IXL accountability form. On this form, students would record which standard they practiced, and what the running score was. Since my old school didn't have D grades and required at least a C grade to be passing, it would be a good idea to require a score of 70. If a score of 70 is attained, the student would earn one participation point. A second point could be earned for a mastery score of 100, so that the student wouldn't just stop at 70 and call it a day. On the other hand, if a student didn't earn 70 due to being lazy or off-task, punishments would begin.

[2019 update: About a month and a half ago, I subbed for a regular teacher who required his students to write all their computer work on a blank sheet of lined paper. This would have served the same purpose as the "IXL accountability form" I describe here -- and also would have put less strain on the Xerox machine.]

For the special scholar, I could work with her one-on-one and double her scores, so that if she were to earn a score of 35, I'd count it as 70 and give her the point. I'd much prefer that she work hard to earn the 35 than just to cheat and earn a 70, or even a 100.

With the IXL accountability form, students without laptops must answer questions. We notice that on IXL, a student must correctly answer at least 11 questions to attain a score over 70. Therefore there would be space for eleven answers on the form. I'd write the 11 questions on the board for them to copy and answer, and all of them must be correct or else they must redo them. This should eliminate students intentionally giving away their computers.

Finally, one problem during IXL time was keeping the laptops organized. I had noticed that the Monday coding teacher would have the students plug the laptops into the cart in numerical order, and I'd tried to do the same with the IXL laptops. (Notice that the coding Monday laptops are not the same as the IXL laptops.)

First of all, I should have taped in laptop numbers to the slots on the cart. This way, I could call the groups in order by readiness, rather than insist that student 620 wait for 602 and over a dozen more students to put laptops away first. Second, I should have come up with a punishment for those who don't put the laptops away correctly. I knew, of course, that simply denying the student a laptop the next day isn't an effective punishment and indeed, may be seen as a reward instead. The IXL accountability form would have taken care of that problem.

Two weeks after the neutral girl moved away, I had a heated argument with the special scholar. I've recorded this argument in my September 26th post:

It begins as my eighth graders arrive. Usually, the coding teacher arrives 20-25 minutes after the block begins, so I use that time for a Warm-Up and passing out the homework for the week, and then the students can use the extra time to start on the homework until the coding teacher gets here. I pass out calculators for the Warm-Up, since it is still on square roots and irrational numbers.

But then the students continue to use the calculators on the homework. The questions on the homework (that come from a practice workbook) aren't quite dren-level questions like single-digit multiplication -- indeed, the first question is long division. But still, this is the type of question that some people (like traditionalists, for example), say should be done without a calculator.

So I take the calculators away. And this causes one student -- and she happens to be the lowest student in the class -- to say, "I need the calculator because I'm not smart like you are!"

I know that from a traditionalist perspective, the people who can do long division by hand are actually the normal ones and those who can't divide are on the outs! I don't bring up traditionalists in class anymore, but I do say, "I'm not smart -- I'm normal."

The girl's response is, "I need it because I'm not normal like you are!"

The girl I mentioned in this post is, of course, the special scholar. The reason that I used the word "normal" was to emphasize that long division isn't something that only nerds should be good at, but everyone should know how to do it. But the special scholar was clearly offended by my use of the word "normal," because I had implied that she, who struggled with long division, wasn't normal.

I proceeded to write about "a Math Intervention block" (that is, IXL time) that same day:

Keep this in mind as I discuss what happens when the eighth graders return after lunch -- a Math Intervention block that also used for an online math curriculum. The girl enters the classroom upset because someone has taken her cellphone, and so she disrupts the classroom by telling the other students to empty out their backpacks in search of the phone.

I tell the students that I can't make them turn in their phones, but I can enforce the rules by at least not granting any class time to search for missing phones. The student begins to cry, thinking about what her mother will say when she finds out that the phone is missing.

Then she tries to ask for a restroom pass -- but the problem is that last week, the principal told me that I can't allow restroom passes anymore either. Formerly I've been allowing students to leave during Music Break, but lately they've been taking advantage and using that time to go places other than the restroom. At this point the girl complains, "I hate this class because you care about the rules so much!"

At this point I tell her that if she leaves, I'll have to give her a detention for using the restroom during class time. (Of course she has no intention of going to the restroom -- she just wants to go out and search for the phone.) She accepts my detention and leaves the room. But then the principal shows up to the classroom, having been called in by the English teacher due to the riot in my class. The principal asks for the girl who first caused the disruption, and upon her return from the "restroom," she is forced to go to the office.

Let's step back now and think about what's happening here. Obviously I was yelling at the special scholar, which is generally a bad idea. I write this in my second New Year's Resolution for 2019:

2. Keep a calm voice instead of yelling at students.

The reason that I enforce the rules is that students who use the restroom only during breaks and puts their education ahead of the entertainment of a cell phone find themselves with lots and lots of A's on their report cards. Given a choice between being bored with an A and entertained with an F, I'd always choose boredom with the A.

Of course, this also goes back to the first resolution. My management was unfortunately not based on how students think. The special scholar asked why she had to follow a certain rule, and I told her it was so she could learn more and earn higher grades. I wrongly assumed that I could convince her to follow the rules by telling her the benefits of learning.

And indeed, this is how I avoid yelling. I yelled at students when I really needed them to follow an instruction and I knew that they'd ignored me if I merely told them the instruction. Instead, if I follow the first resolution, the students are more likely to comply because they'd know that a punishment is coming, and so I can give the students instructions without needing to yell.

I ended that September 26th, 2016 post by writing:

So far, I've seen that endless stories about traditionalists, A's, and their futures doesn't work. And of course, yelling at her as I did today doesn't work at all. Of course, there is no simple answer -- otherwise we'd all be excellent math teachers.

Well, now I understand what I should have done about the cell phone incident -- I should have just called the office. Even though the ideal manager tries to avoid calling the office to send a student out of the room, a distraction such as this one merits an office call. Then the administrators in the office could help the special scholar find her phone and I could get the rest of the class working on IXL.

Meanwhile, I know now what to do to avoid both stories about A's and yelling in general situations (other than a missing phone). I simply let the students know that I'm enforcing the rules, and that I'm enforcing them "because I say so." Teacher tone and teacher look may be helpful to avoid arguments, and live up to the second New Year's Resolution.

2. Keep a calm voice instead of yelling at students.

October 2016

I've said several times that I won't talk about A's so often. But I still plan on continuing my campaign against "drens." In my October 20th, 2016 post -- one of my most extensive posts on "drens" -- I write about my Dren Quiz schedule:

First, with Quizzes now at only 20% of the grade, I'm giving three Dren Quizzes each trimester rather than four. This dramatically alters the way these quizzes work. When I was going to have four Dren Quizzes per trimester and eleven of them the whole year, I started with 10's and then had the students work their way from 2's to 9's. The two extra quizzes meant that if a student fails (which means anything less than an A, or 45/50), that quiz is repeated, while the other students move on.

But now I'm only giving nine Dren Quizzes the whole year. This means that everyone, pass or fail, will be taking the same quiz. Today is the third quiz, so they will work on their 3's. But my "drop the lowest grade" policy applies to Dren Quizzes -- only two of them actually count. This isn't important now with the students working on 10's, 2's, and 3's. But in the third trimester, when the students work on the difficult 7's, 8's, and 9's, this will make a difference.

Indeed, students who fail their 8's quiz -- the most challenging, according to vjlomocso's chart -- can make it up by passing the 9's quiz.

I proceed by discussing the results of the 3's Dren Quiz:

Of course most of my students pass their 3's Dren Quiz today, but unfortunately, three students (two sixth graders and one eighth grader) ended up failing. There are issues with all three students that, due to their sensitive nature, I choose not to post here on the blog.

And of course, you can figure out which eighth grader failed the 3's Dren Quiz -- the special scholar. I didn't want to reveal the "sensitive nature" of the three students being special ed students. And I still don't want to write much about the issue now. All that matters here is that the special scholar failed it.

By the way, she had no problem with her 10's and 2's earlier -- and due to the grading system that I explained earlier, the 3's Dren Quiz failure had no effect on her trimester grade.

But I believe that the 3's failure motivated her to work harder. At the time of the Dren Quiz, the students were learning about roots of perfect squares and cubes. Just like the Dren Quiz itself, the general quiz required the students to memorize, in this case the square and cube roots.

Meanwhile, it was around October when it became obvious that in my students' eyes, I was below my support staff member on the totem pole. By this, I mean that often students would talk throughout my lessons, and then stop talking only when she arrived. To them, directions from me didn't count -- they only mattered if the support aide or someone else was giving the directions.

This happened one day during a lesson on exponents -- the class was talking during my lesson and stopped only when the support aide arrived. I was upset -- I knew that the students would never learn anything from me if they believed that only her directions counted. And so I called the students out on it and asked, "How come you can't be this quiet when I am teaching?"

The special scholar's replies went something like, "Well, we're quiet now!" and "Why are you wasting time instead of teaching the lesson?"

The third New Year's Resolution for 2019 refers to the mistake I made with this interaction:

3. Move on from past incidents instead of bringing them up with students. 

In this case, once my support aide arrived, the talking was in the past. Bringing it up again did nothing to the solve the problem.

Obviously, my concern wasn't about the past but about the future -- I knew that the next time my support aide left the room, the students would start talking again.

Because of this, my interactions should have dealt with the present and future. Here is what I could have said that would be more in line with the third resolution:

"Good job! The class is now silent. This is what I want the class to sound like the next time our support aide leaves the room."

At this point, I can test the students on this. I can send my support aide on an errand for any random reason -- it could be just to photocopy more Warm-Up sheets. Now I expect the students to start talking again the instant she leaves the room -- indeed, I reckon the first bold student will talk as soon as soon as she opens the door, even before she's actually left. So before she leaves, I say:

"This counts as a warning to the entire class. Anyone who talks will receive a punishment."

When my support aide opens the door to leave and the inevitable occurs, I give the punishment. Then I ignore any protests that the punishment is mean or unfair, since I do make it clear what noise level I desire (namely silence) and what will happen if anyone talks (a punishment).

The third resolution reflects back on the first two resolutions. I don't yell at the student who talks (second resolution), but stick to a solid management plan (first resolution).

Of course, since I didn't do this, in the end the students struggle with exponents. Fortunately, an easier lesson was around the corner -- memorizing basic squares, cubes, and roots.

I gave the general quiz a week after the Dren Quiz, on October 27th. But I didn't write about the results of the quiz until November 1st:

After the final Exit Pass, my support staff member bought a pizza for the eighth grade class. This is to celebrate the scores on their most recent Quiz #3 -- of the thirteen students, ten students received A's and the other three earned C's. The square and cube roots were fairly easy to memorize -- let's see whether they'll be able to maintain their success as we move on to more difficult topics.

And the special scholar was one of the three who earned C's. After the disappointing Dren Quiz, a C on the general quiz was great! I gave the students, in addition to my support staff member's pizza, some Halloween candy as a reward. Each student with an A earned four Tootsie roll pops. Usually the C students earn no candy, but I gave the special scholar one Tootsie roll pop anyway because I knew that she'd worked hard to learn the square and cube roots.

By the way, going back to old posts again, one of my earliest uses of the word "dren" on the blog was back in January 2015:

So I need a word that criticizes the student, yet is proper for me to use in a classroom. Well, since I want my word to have the opposite effect of the word nerd, I briefly mentioned at the end of one of my posts a few months back that I made up my own word, by spelling the word nerd backwards, to obtain "dren."

My plan is to use my new word "dren" in such a way to make it sound as if a "dren" is not what a student wants to be. For example, when we reach the unit on area, students will need to multiply the length and width to find the area of a rectangle. So I might say something like, "A dren will have trouble multiplying six inches by nine inches. Luckily you guys are too smart to be drens, so you already know that the area is ...," and so on. Similarly, if a student, say, starts to reach for a calculator to perform the single-digit multiplication. I can say, "You're not a dren. You know how to multiply six times nine ...," and so on.

Notice that in these examples, I don't call anyone a dren directly. But every time I say the word "dren," I want to be annoying enough so that the students will want to do what it takes to avoid my having to say that word.

This is still how I want to use the word "dren" in my classes. I want my students to know that they are too smart to be drens -- including the special scholar. I want to use the word to make them feel smarter, not less smart. So far, my use of the word really did motivate the special scholar to do well on the roots quiz.

Then again, maybe she and the rest of the class would have fared better on the previous exponents quiz if I'd formulated and followed the third New Year's Resolution:

3. Move on from past incidents instead of bringing them up with students or flouncing around.

[2019 update: About a month ago I subbed in an English class. The word "flounce" appeared on a vocabulary quiz, meaning "to go or move in an exaggeratedly impatient or angry manner." I realized that in addition to yelling at the special scholar and other students, I might have been flouncing at them as well. I add this to the resolution to ensure that I don't make sudden body movements that students may find alarming.]

November-December 2016

I never mentioned this on the blog, but when the first trimester ended in November and the students were about to get their report cards, I decided to reveal my own middle school grades. I actually still my old report cards from those grades. Naturally, I showed the sixth graders my Grade 6 report card, the seventh graders my Grade 7 report card, and the eighth graders my Grade 8 report card. My old school graded using quarters, not trimesters -- but that's okay, since I've saved only three report cards from each year anyway. For Grade 7, these were my second quarter grades (since I don't have the first quarter grades), while for the other two years, these were my first quarter grades.

Here are the grades that I revealed:

6th Grade:

Language Arts -- A

Spelling -- A

Math -- A

Social Studies -- A

Multi-Cultural Arts -- A

7th Grade:

Art/Shop -- B

Success -- A

P.E. -- A-

Algebra I -- A+

English -- A

History -- A

8th Grade:

Science -- C

History -- B+

P.E. -- B+

French I -- A

English -- B+

Geometry -- A+

My original intention was to show the students my second quarter marks at the end of the second trimester in March, and then my final marks at the end of the year. But of course, I didn't quite make it to the end of the second trimester.

In my November 10th, 2016 post, I wrote about how my eighth graders fared that first trimester:

Of course, the end of the trimester means giving out grades. As it turns out, none of my eighth graders is failing this first trimester. There were a number of easier topics this first trimester -- and I've said before that I like the idea of giving the students grades before the hard topics come up. This way, students can feel good about themselves and believe that they can succeed in the new trimester on the more difficult topics.

The lowest student in the class managed to scrape barely with a C (recall that there are no D's). I know that she worked hard to pass the last quiz on exponents -- I'm so proud of her! Meanwhile, one guy has emerged as the new top student in the class, and so he easily earned an A this trimester.

I don't quite remember who the "new top student in the class" was. It might have been the eventual valedictorian, but it could have been one of the other guys in the class.

But we can easily figure who "the lowest student" was -- the special scholar. As we see, that last quiz allowed her to pass the class with a C. Recall that at this point, I hadn't taught much science yet. The grade I assigned the students appeared on the report cards as a "STEM" grade -- meaning that both math and science were included in the grade.

By this time, the Pappas-style Warm-Ups had fallen apart, and Illinois State Daily Assessments were now the norm. Since the answers weren't always the date, these computer questions that I projected on the board were more challenging -- especially when I clicked on "hide multiple choice answers."

Of course, when I didn't give them a stamp, the girls would complain that I was mean and unfair -- that I wasn't giving them the stamp because I didn't "like " them. And then they would hold up the class until I relented and give them the stamp. Other students in the class -- sometimes even other members of their clique -- were upset that I was taking too long with the Warm-Up, which after all the arguing was now spanning 10-15 minutes.

This incident was what I had in mind when I formulated the fourth New Year's Resolution for 2019:

4. Begin the lesson quickly instead of having lengthy warm-ups.

 
Here is what I should have done with the Warm-Ups. First of all, Pappas-style questions whose answer is the date are to be reserved for Exit Passes -- that is, I should have established the Illinois State Warm-Ups from the very start. Illinois State recommends that the Daily Assessments take about five minutes. Now when I first introduce the Warm-Ups, I give the following reminders:

• Let's begin the Warm-Up. You have five minutes.
• There are four minutes to go, yet some of you don't even have a pencil out.
• There are three minutes to go, yet some of your Warm-Up sheets are still blank.
• There are two minutes to go, yet some of you have barely started.
• There is one minute to go. Double-check becayse only correct answers get stamped.

Now the special scholar and her friend receive sufficient warning that they should stop talking and start writing. There's less room for them to complain that I didn't give them enough time.

Unfortunately, I got into more arguments with her that week. I mentioned this back in my November 18th "Day in the Life" post. It goes without saying that the girl in this post was the special scholar:

• On Monday, an eighth grader complained about the Parent Conference week schedule. Nutrition is at 11:05 everyday, but this is after two periods on regular days and three on shortened days. (Other middle schools often do the same -- they have break after 2nd period most days, but after 3rd period on shortened days.) She insisted that it was break and that I couldn't tell time, so I yelled at her.
• On Thursday, the eighth graders were doing a science lesson with my Bruin Corps member (again, see yesterday's "Day in the Life" post). This was a life science lesson, but it appeared in the eighth grade standards according to our online software. One girl (yes, the same girl from Monday) correctly noted that she learned this lesson in seventh grade (under the old pre-NGSS standards) and therefore she'd refuse to work on the lesson. I was about to login to our website and show her the standards, but she continued to complain before I could get to the site, so I yelled at her again.

Later in that post, I wrote about how I should have avoided the Monday argument (and uphold the eventual second resolution, "no yelling"):

Let's look at, for example, Monday's argument and how I could have avoided yelling at the eighth grade girl:

Me: After this class you will go to English class.

Girl: No, we have nutrition now.

Me: For a participation point, who can read me the schedule written on the board?

Another Student: After this class we go to English.

Me: Thank you. You get a point.

That ends the argument, since now it's no longer me against the girl, but me and another against the original student. The other student is given an incentive -- the participation point -- to side with me and the correct schedule instead of the girl saying the wrong schedule.A similar trick could have worked with the same girl on Thursday. I ignore her when she says that she won't do the science lesson and have another student read the standards from the website. It's even possible that the original girl wouldn't have contradicted me on Thursday -- she might have shown me more respect, because I'd have shown her respect by not yelling at her on Monday!

In subsequent posts (after I learned more about the California Science Test), I wrote that I probably should have focused on physical science (the old standards) with the eighth graders. Likewise, I could have taught life science (the old standards) to the seventh graders. Only to the sixth graders could I have taught the new NGSS standards.

This solves the problem and avoids the Thursday argument. But as I wrote in that post, instead of gaining her respect on Monday, I had lost it. The special scholar would never respect me again from that day on. She might have respected me more if I had kept the fourth resolution:

4. Begin the lesson quickly instead of having lengthy warm-ups.

I wrote that the top student at the end of the first trimester wasn't necessarily the eventual valedictorian. Indeed, several boys in the class could have emerged as the valedictorian. But unfortunately, there weren't as many girls with top grades -- especially not the clique girls.

The other was a new student who joined the class right after Thanksgiving. She quickly became one of the top students in the class. She told me that at her old school, she was in an Algebra I class, and so she'd already learned everything that I was teaching.

But I really wanted to make sure that the new girl could get into Geometry next year. After all, she'd been already enrolled in an Algebra I class at the start of the year. I didn't think it would be fair for her to have to repeat Algebra I as a freshman just because she attended our school. I wanted to do for her what I couldn't do for the neutral girl -- actually teach her Algebra I during IXL time, so she could do well and I could prepare her for Geometry. But I had to wait until the administrators added her name to the IXL roster. After all, IXL accounts weren't free, and thus there were strict controls on who could have an account.

Why did the new girl care about the special scholar so much? That's easy -- the girls were cousins.

On the other hand, cousins are more likely to be of the same age and grade level. Indeed, several girls in the seventh grade class were cousins. None of these cousins are related to the eighth grade duo, the focus of this post.

This shows how I could have improved interactions with the special scholar. Each morning, I could have waved to the special sister ("special sister" = "special scholar's sister"), and perhaps even said "Hello," addressing her by name. As a teacher with dozens of students, I can't be expected to know the siblings of all of my students, but I could have at least gotten to know the special sister, especially since I saw the two girls walking to school every morning.

But let's return to the special scholar and the special cousin. The two cousins were seated together, along with the girl who was the leader of the clique.

Oh, and speaking of cousins, this is something that traditionalists might want to heed. Traditionalists like to point out that teachers don't spend enough time thinking about the top students, instead focusing on the weaker students. They say that it's much better for teachers to satisfy the needs of the top students, even if it means ignoring the weaker students. After all, the top students are the future "heroes" who will make our lives better.

Incidentally, the traditionalists will like that the special cousin did ask me why there weren't separate Common Core 8 and Algebra I classes. (The answer, of course, is that there only 14 eighth graders, and we'd hire a science teacher before a second math teacher.) The top student asked me this, even though she knew that if there were two math classes, she'd surely be separated from her cousin, the special scholar.

The week after the new student arrived, I gave a test on volumes of cones and cylinders. I wrote about how the students fared on this test in my December 12th, 2016 post:

Then right after the holiday was the first test of the trimester, and I had to give even more zeros for talking and cheating. Here's how I caught two of my eighth graders -- do you recall the eighth grade test on volume? The problem was that many of my CASIO calculators would convert decimals like 3.14 to fractions, while others would keep them decimals. In fact, one CASIO did neither of these -- instead, it gave answers as mixed numbers. There was only one such calculator, and I knew exactly who had it -- yet three students tried to turn in tests with mixed number solutions!

As it happened, the student with the mixed number CASIO was the special cousin -- and I knew that she was smart, so she didn't need to copy from anyone. One of the cheaters was the girl sitting next to her -- the special scholar. The other cheater was one of the other clique girls who sat at the next table, yet was close enough to copy the answers.

Meanwhile, the other student who sat with the second cheater was yet another clique girl. She had left much of her test blank and told me that she didn't get it. Of course, since the answers were blank, she hadn't been involved in the cheating. I didn't like the idea of giving her a score of 50 while the cheaters had copied enough answers to score a 60. So I had to give both cheaters -- including the special scholar -- a score of zero.

When I grew up, I developed some bad Schadenfreude habits. Many exhibit Schadenfreude from time to time, but it's not good for a teacher to exhibit it when a student struggles. I'm so afraid of showing anything that looks like Schadenfreude that I try to stop myself from laughing at all in class.

The special scholar spotted me. She saw me struggling not to laugh -- and it suddenly became a new game for her and some of the other clique girls. They would start saying random things or looking at me weird. I'd start to laugh, and then they'd reply, "I see you laughing!"

It's understandable that the special scholar would struggle with the volume test, but I believe the other girl should have fared better without resorting to cheating. This could be because of how I taught the lesson -- which leads to the fifth New Year's Resolution for 2019:

5. Engage the students in the learning process instead of lecturing excessively.

Here's what happened -- on the day of the traditional lesson, I would ask the students to listen and answer questions, but they talk and do very little work. Then just before the test, there would be a "review" day. I asked the students to solve a volume problem -- but since no one had paid attention, they didn't know how to do the first strp. Desperate to see 14 hands writing something down, I'd just do the entire problem on the board and ask them to copy. This is what "lecturing excessively" refers to here -- having the students copy entire problems on so-called "review" days.

Of course, some students might still be hesitant to participate. I should have used Sarah Carter's and Christie Bradshaw's dry erase packets in order to help the students learn the material. This would have helped the other students immensely, including that clique girl who gave up with a 50, and the other clique girl who cheated. This would have freed up time for me to assist the special scholar.

One December day during IXL time, some eighth graders started playing with the lights -- and a few seventh graders who had come in to borrow laptops for English class joined them. I knew that I had to punish the students who were involved, and I ended up yelling at one of them. It ended up being -- who else -- the special scholar. Even though she really was involved with the lights, there was no reason to single her out in this situation.

I remember that the special girl cried, and she told her friends that for some reason, many teachers had singled her out for no reason -- I wasn't the only one. I became so upset that I decided to buy her a bag of her favorite candy -- Jolly Ranchers.

The momentum the special scholar once had when she passed the October quiz was gone. But if it's any consolation, she at least passed her 4's Dren Quiz in December. The history teacher had given me the idea of cutting the Dren Quiz in half for struggling students. This worked, since she did very well on the reduced 4's Dren Quiz. And this is despite the 4's being much more difficult than the 3's, according to vjlomocso's chart from earlier.

The history teacher had planned on giving the students a party on the last day before winter break, but he cancelled the party as punishment for playing with the lights. (This would have been the day of the Kwanzaa Karamu.) But the special scholar claimed that the party wasn't cancelled, and shared a bag of chips with me -- which I ate, which "proved" (from her perspective) that it really was a "party" after all. The special cousin contributed to the "party" by playing some rap music on my laptop.

This ended a rocky December -- and it all started with the problems I had with the volume lesson. In order for students to learn more effectively, I must keep the fifth resolution in mind:

5. Engage the students in the learning process instead of lecturing excessively.

January-February 2017

Both the special scholar and special cousin tried to neuter more of my rules. In this case, the special cousin was actually worse than the special scholar! The special cousin really wanted to neuter the "no cell phone" rule, and she accomplished it. First, she told me I was wrong to make her sit in her assigned seat, and so she should be allowed to sit in my support staff member's seat (on a day when my support staff member was not present). There she covered herself with a blanket and started texting on her phone. And of course, if I told her to put the phone anyway, she'd claim that since she was hidden, I couldn't prove that she actually had a phone.

Is there anything I could have done so that the special cousin would've been happy to follow rules and show me how smart she was at math instead of just outsmarting me with the rules? The answer is simple -- I should have treated her cousin, the special scholar, better before her arrival. Then there would have been less reason for the special cousin to dislike me from the start.

One day I tried to give a science lesson. I wrote about it in my January 13th, 2017 post:

But first, let me provide some explanation. My small charter school has no middle school science teacher -- instead, I, as the math teacher, must include some science into the lesson. Notice that some STEM projects, like the ones I gave sixth and seventh, already contain some science. But I want to be sure that the eighth graders receive sufficient science content since this is a tested subject here in California.

But then one girl -- the top student in math -- begins to complain. She argues that at the very least, science should be project-based, and so she wants to have some project rather than a worksheet. I assume that she had her hopes up all week when she saw that we'd be doing science, only to be disappointed when she sees the worksheet today. She says that she enjoys the science projects that she performed at her old school, before she transferred to our school over a month ago.

The "top student in math" refers to the special cousin.

Similarly, they weren't looking forward to the Hidden Figures movie (which was released two years ago on Epiphany, by the way), just because I was the one recommending it to them. They told me that they planned on texting during the entire movie (even though that's against theater rules). Anything I liked, they would hate.

The sixth New Year's Resolution for 2019 states how I should have handled the science problem:

6. If there is a project-based curriculum such as Illinois State, then implement all components of it.

After all, Illinois State provided an online science curriculum in addition to math. I've spent several posts discussing other ways I could have taught science better -- most notably searching for the LAUSD pacing plan to handle the transition to the Next Generation Science Standards. Bruin Corps and Green Team were not substitutes for the true science curriculum in the Illinois State text.

Leading up to the Dren Quiz, I sang a new song called "No Drens," a parody of TLC's "No Scrubs." I set up the song by explain that both "drens" and "scrubs" are losers who don't have enough basic skills to be hired for jobs.

The special scholar was clearly offended by this statement. She started telling me about an older cousin who was a doctor. "She can't read small print, but she's got a better job than you!" It's obvious what was going on -- even though I didn't give any names, the special scholar saw herself in my statement about people who lacked basic skills, which is why she was so offended. And of course, it goes without saying that I shouldn't respond to her comment by yelling at her (second resolution).

Instead of arguing, I just started singing the "No Drens" song. In the end, the song was one of the special scholar's favorites -- one of the first songs she liked since September.

Again, to make sure that my students have a chance to learn everything in the curriculum, I must keep the sixth New Year's Resolution in mind:

6. If there is a project-based curriculum such as Illinois State, then implement all components of it.

In my February 18th, 2017 post, I wrote the following reflection:

3) We are reminded constantly of how relational teaching is.  As teachers we work to build relationships with our coworkers and students.  Describe a relational moment you had with someone recently.

This week was Valentine's Day -- a day strongly associated with relationships. Lately I fear that I've been criticizing certain students too often.

In fact, one eighth grader has had enough of all of this. I got upset at her this week when I passed out Valentine's pencils and she decided to take two pencils for no reason. She eventually apologized, but she rejected my own apology for lashing out at her -- probably because she correctly notes that I'll end up yelling at her again at some point. At least I acted like the adult I should be by accepting the girl's apology. But her actions show that it's too late to repair my relationship with this student.

By this point, do I even need to identify the eighth grader in this incident? It goes without saying that the girl mentioned in this post is the special scholar. And it was right after her birthday, to boot -- her special day fell on the weekend, and this incident occurred on a Monday.

In reality, the special scholar was just being oppositional. I wanted her to have exactly one pencil -- so she preferred to have either zero or two pencils, anything other than the exact number that I desired for her to have. Anything I wanted, she didn't want.

The final Dren Quiz that I gave before I left the school was the 6's. According to the chart, this was the most difficult row of the table among those that I quizzed on. Yet the special scholar passed her 6's as well, despite having failed her 3's. I think she was so embarrassed after failing the 3's that she worked hard to ensure that she'd pass the bigger numbers.

But before she left, the special cousin told me that I was a good singer -- after a music break. I recognized this as the back-handed compliment that it was. She was really saying that I should have been a singer instead of a teacher, because I wasn't a great teacher. I didn't say this out loud, though, since I'd have gained nothing good from saying so.

It was a Wednesday, and the students had a SBAC Prep lesson. There were many "review" questions on exponents, and some students -- including the special scholar -- complained that they don't "remember" how to solve the exponent problems. But as I wrote earlier in the October section of this post, they never truly learned exponents in the first place.

But there is one more resolution to mention here -- the seventh New Year's Resolution of 2019:

7. If there is an official assignment to review for state testing, then implement it fully.

In reality, the students shouldn't have been answering my questions in the first place. Instead, they needed to take out the laptops and try the practice problems directly from the SBAC website.

Even after I finally had the students try the practice tests, I didn't realize, for example, that some of the questions forbade a calculator while others allowed it. This would have been a great time to figure out how to use the embedded calculator (powered by Desmos).

By the way, I never did look up my old school's released SBAC scores, and so I decided to do so in time to write this post. The scores are difficult to decipher for two reasons:

• Our charter school's results are combined with our sister charter's results. So it's difficult to tell which scores belong to my students and which scores belong to students I never taught.
• Our charter school is so small that many categories end up being hidden by asterisks (fewer than ten scores reported) to protect student privacy.

For example, our sister charter had no eighth graders, so it's safe to conclude that all eighth grade scores came from our campus. But only 11 eighth graders took the English test -- and all it took was one of those students to be absent on the day of the math test for an asterisk to block it. (The same thing had happened to this cohort the previous year -- 12 seventh graders took the English test, but at least two of them were absent for the math test.)

As it turns out, our sister charter school is almost 100% black (yes, another vacation post mentioning race), while our school has a few Hispanic students. Therefore I can use "Hispanic/Latino" as a proxy for "was taught by me rather than the sister charter."

The only grade with enough Hispanic students not to be blocked by an asterisk was seventh grade (as I mentioned in previous posts). Here are the math scores -- there were 13 students. One earned a 4 (the highest score -- only PARCC goes up to 5), two earned 3, two earned 2, and the rest had 1. By the way, I have a good feeling as to which student earned the 4.

Comparing all the sixth and seventh grade scores to the previous year, the scores were mostly flat. I see a very slight increase -- but it can be attributable to a single high scorer being added to each cohort, a 3 scorer in sixth grade and the aforementioned 4 scorer in seventh grade. (If the 3 scorer was at our charter, then I think I know who it is. But on November 8th, 2016, when I visited the other campus, I remember a smart sixth grader who might also be the 3 scorer.) Of course, since my students were talking and not learning, my successor teacher should get the credit for keeping the scores flat (since math scores tend to decrease as students get older). I might be able to claim credit for maintaining or even raising the scores had I followed the seventh resolution:

7. If there is an official assignment to review for state testing, then implement it fully.

There is better news in the score report for our English teacher. The highest increase in average ELA scores was for the seventh grade. Even though there were seventh graders at the sister campus, this group was small, so most of the credit goes to our English teacher. The seventh graders might have driven her crazy, but they learned a lot from her too.

In my March 20th, 2017 post, I wrote the following reflection:

Along with the pizza, I'd left a personalized "Good Luck" card for each student. I'd originally planned on giving each student such a card on the last day of school, but due to the circumstances I decided to hand out the cards right then on Pi Day.

And this is what I wrote on the special scholar's "Good Luck" card:

"You are not a dren. You never were, and you never will be. Keep this in mind, and you'll be successful in math from now on. Good luck in high school!"

When I'd first met the special scholar at the start of the year, I was hoping to be the math teacher that she'd remember in a good way. Perhaps five or ten years from now, she could have said something like the following:

I was never good in math until I took Mr. Walker's class. He made me work hard, but I learned a lot in his class. I'm much better at math because of him.

Of course, she'll never say that now, because it never happened. Instead of inspiring her to learn math more, I did the exact opposite.

Ever since I left the school, I missed being there for my students. But the one student I thought about more than any other was the special scholar. I believe that if I had built a better relationship with the special scholar, I would have done better with the other students -- and then I would never have had to leave the school.

As I return to the classroom as a sub, I will always remember the special scholar -- and I'll make sure to work harder to earn the respect of the special scholars in my new class. And to do so, I must keep all seven New Year's Resolutions for 2019:

1. Implement a classroom management system based on how students actually think.

2. Keep a calm voice instead of yelling at students.

3. Move on from past incidents instead of bringing them up with students or flouncing around.

4. Begin the lesson quickly instead of having lengthy warm-ups

5. Engage the students in the learning process instead of lecturing excessively.

6. If there is a project-based curriculum such as Illinois State, then implement all components of it.

7. If there is an official assignment to review for state testing, then implement it fully.

David's Lunar Calendar

OK, let's finally construct that new lunisolar calendar I referred to in my last post. For a starting point, let's refer to the following link:

http://calendars.wikia.com/wiki/Lunisolar_calendar

We're trying to follow Paul Rapoport's suggestion that we include the number 12 and as many multiples of 12 as possible. If we scroll down to the "Cycles" chart at the link above, the first row mentions a 19-year cycle -- the Metonic Cycle.

In that chart, there's only one multiple of 12 listed there -- a 372-year cycle. So voila -- that's the cycle for my new calendar. The number of days in this cycle is 135870 -- though not a multiple of 12, it is a multiple of six. So we'll double this to a 744-year cycle. As we'll see soon, there's another good reason to use 744 rather than 372 years.

Now let's set up the number of days per week and month for this calendar. In my last post, I referred to the effects of a possible 12-day week. Well, Rapoport wanted to see lots of 12's in this calendar, so let's select the 12-day week.

I mentioned that unlike the 8-, 9-, and 10-day weeks, a 12-day week applied to the solar calendar would require us to skip days. There's an existing 6-day calendar where a day is skipped in 365-day years: the Double Rainbow Calendar:

http://calendars.wikia.com/wiki/Double_Rainbow_Calendar

But this is a lunar calendar, so perhaps we wouldn't need to skip days. Notice that here, long years with 13 months (with 30 days in the leap month) have 384 days, and guess what -- 384 is indeed a multiple of twelve! On the other hand, 12-month years contain 354 days, which isn't a multiple of 12, but is a multiple of six.

Now hold on a minute -- the reason I wrote about longer weeks in my last post is that I wanted the year to contain half weeks, because of birthdays! We didn't want anyone's birthday to be stuck on the first day of the workweek, and a year with half-weeks would make someone's birthday fall on weekdays every year. So we can use the fact that the common 354-day year contains half-weeks to our advantage.

Notice that there are 12 days in a week as well as 12 months in a common year. If we use the normal 30, 29, 30, 29 (or vice versa) pattern for lunar years, then we can make each of the 12 months start on a different day of the week.

Let's start by naming the months. For lack of better names, we'll use colors just as in the Double Rainbow Calendar:

Month    Name
1             Violetlong
2             Violetshort
3             Bluelong
4             Blueshort
5             Greenlong
6             Greenshort
7             Yellowlong
8             Yellowshort
9             Orangelong
10           Orangeshort
11           Redlong
12           Redshort

Months ending in "-long" are long months of 30 days, while months ending in "-short" are short months of 29 days. That should be easy to remember.

Now the order of the months follows Double Rainbow Calendar. Palmen doesn't explain why he chooses this sequence, but we can imagine why. "Violet" and "blue" are cool colors associated with the winter. "Green" is the color of spring leaves. "Yellow" and "orange" are the color of the summer sun. And "red" is the color of autumn leaves. (But Australians and others in the Southern Hemisphere might object to these season colors.) At any rate, this tells us that Violetlong, the first month of the year, should probably be around the time of the winter solstice.

In Palmen's Double Rainbow Calendar, the days of the week match the months, so that each month begins on the day of the same color. His calendar is a solar calendar based on 30's 31's, and 61's, and so the first of the month advances throughout the week. In other words, his day colors and month colors are in the same order. But my calendar is a lunar calendar based on 29's, 30's, and 59's. The first of the month retreats throughout the week, and so our day colors must go in the opposite order from the month colors:

Day        Name
1             Redday
2             Orangeday
3             Yellowday
4             Greenday
5             Blueday
6             Violetday
7             Redend
8             Orangend
9             Yellowend
10           Greenend
11           Bluend
12           Violetend

Days ending in "-day" are weekdays, while days ending in "-end" are weekends. That should be easy to remember. All birthdays switch between weekdays and weekends in common 354-day years, so if your birthday is on Redday this year, then next year it will fall on Redend.

But 384 is a multiple of 12, so if your birthday is on Redday and it's a long year, then next year it will fall on Redday again. But in two years it will fall on Redend. Since there are never more than two long years in a row, you can never have more than two consecutive weekday birthdays either.

Since Violetlong is the first month of the year, the year must start on either Violetday or Violetend every year. This makes this calendar a rare one in which New Year's Day can never fall on the first day of the week in that calendar. But I wanted the day colors to run in the opposite order from the month colors. Thus the first month must begin on the last day of the week, while the last month starts on the first day of the week.

This is one of those calendars for which the weekend is fully half the week. Six days of work in a row might be tough, but it might be worth it for the six-day weekend! Or otherwise, we can follow the same pattern as my Eleven Calendar, with a day off right in the middle of the week. If we choose Greenday as the mid-week holiday, then the workweek becomes Redday-Yellowday, Blueday-Redend. In this case, Redend would be like our Friday -- it's a workday, but it starts the weekend (so at least those with red birthdays get to celebrate when they fall on Redends). It also means that those with green birthdays would never work on their birthdays. (It also might be nice to place holidays on green days.)

Anyway, let's set up a Metonic cycle based on remainders upon division by 19. Suppose we were to start with a long year:

Year  Months  Starting on
0       13           Violetend
1       12           Violetend
2       13           Violetday
3       12           Violetday
4       12           Violetend
5       13           Violetday
6       12           Violetday
7       12           Violetend
8       13           Violetday
9       12           Violetday
10     13           Violetend
11     12           Violetend
12     12           Violetday
13     13           Violetend
14     12           Violetend
15     12           Violetday
16     13           Violetend
17     12           Violetend
18     12           Violetday

Notice that there are four long years starting on Violetend (years 0, 10, 13, 16), and the Gaia calendar adds four extra days every Metonic cycle. So just add the four extra days to these particular years. This actually makes the calendar more like the Meyer-Palmen Solilunar Calendar, where the extra days are added to years that are already long. (In other words, both my calendar and the MPSLC has years of 354, 384, 385 days while the Gaia calendar has years of 354, 355, 384 days.) The extra day is considered a blank day with no day of the week (that is, no color).

We might place the leap month in the summer -- say Yellowleap, a 30-day month between Yellowlong and Yellowshort. If the year starts on Violetend, then Yellowlong starts on Yellowend, Yellowleap starts on Yellowday, and Yellowshort starts on Yellowend. So we can have the rule "If the leap month causes both Yellowlong and Yellowshort to start on Yellowend, then a blank day should be added."

Since birthdays are so important to my calendar, we ask, when do people born in the leap month celebrate their birthdays in short years? (I wonder the same thing for the Hebrew Calendar -- when do those born in Adar I or Adar II celebrate their bar mitzvahs if there's only one Adar in their 13th year?) I'd suspect that Yellowleapers might celebrate on the same day in either Yellowlong or Yellowshort -- whichever one's on the weekend! (In short years, days in Yellowlong and Yellowshort are opposite.)

We then follow the rest of the Gaia calendar. Blank days are skipped once every 57 years just like Gaia. But Gaia adds a blank day back every 798 years. Since 798 is so close to the cycle length of my new calendar (744 years), we'll change 798 to 744. This means that an blank day is added back every 744 years.

Now 744 years equals 39 Metonic cycles plus an extra three years. These three years look just like the first three years of the cycle -- a long year followed by two short years. As we just found out above, the extra three years must contain one blank day.

Notice that 744 is a multiple of 12 -- indeed, it's 12 * 62, or 6 * 124. This means that the solar part of this calendar is equivalent to the Usher Calendar -- a leap week calendar that I posted three years ago.

When should Year 0 of this calendar be? We wrote above that Violetlong should start near the winter solstice. Most lunar calendars start at the new moon. And since this calendar starts with a long year and contains another long year two years later (Years 0 and 2), Year 0 should be a year that starts early -- say on the new moon preceding the winter solstice in a year when the solstice occurs just before the full moon. This is the earliest the year can start, about half a month before the winter solstice. (The latest it can start is about half a month after the winter solstice.)

It turns out that in 1980, the winter solstice was about an hour before the full moon. And so it works out that Year 0 of the calendar should be December 7th, 1980. Therefore, just as I mentioned in my last post, David's Lunar Calendar really is inspired by the new moon that occurred on the day I was born.

Let's look at the QNTM calendar reform list for properties of the David Lunar Calendar

https://qntm.org/calendar

(x) nobody cares what year you were born

I suspect that QNTM actually had in mind calendars that start in 1969, which was the year of the moon landing. The Gaia calendar starts in 1970. But there's no evidence that those calendar creators were actually born in 1969 or 1970.

But I'm saying it right now -- I was born on December 7th, 1980. This might be the only calendar to which this line truly applies. But then again, I couldn't help but notice the coincidence of the winter solstice and full moon in 1980.

The following apply to almost all lunisolar calendars:

(x) solar years are real and the calendar year needs to sync with them

(x) the lunar month cannot be evenly divided into solar days
(x) the solar year cannot be evenly divided into lunar months

Here are some other features of my calendar:

(x) having one or two days per year which are part of no month is stupid
(x) your name for the thirteenth month is questionable

All lunisolar calendars have a 13th leap month. I assume that all possible names for the extra month are questionable (including my own "Yellowleap").

Actually, I never state whether my blank day is part of Yellowleap or no month. But it definitely has none of the 12 days of the week, so we know we must mark these:

(x) every civilisation in the world is settled on a seven-day week
(x) having one or two days per year with no day of the week is asinine

Since my calendar refers to the winter solstice, we must mark:

(x) not every part of the world has four recognisable seasons

Finally, nearly every lunisolar calendar would marks the following:

(x) date arithmetic needs to be as easy as possible

since division by 19 (for the Metonic cycle) isn't considered easy.

Finally, let's return to the calendar that Nirvana was trying to create. His/her lunisolar calendar can't start on September 22nd every year. But let's rewrite Nirvana's months (with the correct 29- and 30-day lengths):

1. Unary (Sep 22-Oct 21), lasts 30 days
2. Binary (Oct 22-Nov 19), lasts 29 days
3. Ternary (Nov 20-Dec 19), lasts 30 days
4. Quaternary (Dec 20-Jan 17), lasts 29 days
5. Quinary (Jan 18-Feb 16), lasts 30 days
6. Senary (Feb 17-Mar 17), lasts 29 days
7. Septenary (Mar 18-Apr 16), lasts 30 days
8. Octal (Apr 17-May 15), lasts 29 days
9. Nonary (May 16-Jun 14), lasts 30 days
10. Decimal (Jun 15-Jul 13), lasts 29 days
11. Levimal (Jul 14-Aug 12), lasts 30 days
12. Dozenal (Aug 13-Sep 10), lasts 29 days
13. Baker's Dozenal (Sep 11-21)

Then this indicates the range in which each month can begin. Thus Unary can start as early as September 22nd and as late as October 21st. Binary can start as early as October 22nd and as late as November 19th, and so on. If in a given year, there's a month that starts between September 11th and 21st, then it's Baker's Dozenal -- otherwise that year has no leap month.

By the way, Nirvana never states whether each month starts on the new moon. It just so happens that on the proleptic Gregorian Calendar, September 22nd, 36 CE (the year that Nirvana's calendar begins) is a full moon, so perhaps this is a calendar where months start on full moons. If this Year 0 is a long year (with Year 2 a long year as well), then years start on the full moon on or after the fall equinox (in the September 22nd-October 21st range, just as we stated).

Oh, and notice that 36 CE is not a Halley's Comet year, as Nirvana claims. Instead, the comet approached earth in 66 CE. There was a full moon a few days before the fall equinox in 66 CE as well, Nirvana might choose to change the start date to 66 CE.

New Year, Same Old Traditionalists

Yes, 2019 has just barely begun and the traditionalists are back at it already. This is what Barry Garelick posted on New Year's Day:

https://traditionalmath.wordpress.com/2019/01/01/how-is-understanding-measured/

I have written about understanding in math, and the education establishment’s view of it. With all this talk about how it is important for students to “know math” and not just “do math” the question arises: “How do we measure a student’s understanding as opposed to their ability to go through procedures?” That is, how do we differentiate someone who truly understands from that of a “math zombie”.

Garelick addresses several issues in this post. Either he or another traditionalist has alluded to the following college placement problem in the past:

On a placement test for entering freshmen at California State University, a single item on the exam correlated extremely well with passing the exam and subsequent success in non-remedial college math. The problem was to simplify the following expression. (Multiple choice test):  

The argument here, of course, is that this is the sort of problem Garelick wants to see more of in high school math. Even though simplifying rational expressions appears in Common Core Standards, it's probably not emphasized as much as the traditionalists desire. The (+) sign in the standards implies that this will likely be delayed to Precalculus, while the traditionalists would like to see it in Algebra II.

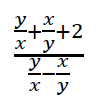
It's easy to see why the Common Core doesn't emphasize rational expressions -- of course students will start asking "When will I ever use (y/x + x/y + 2)/(y/x - x/y) in real life?" and more importantly, leave a p-set full of such problems blank.

Afterwards, Garelick returns to that perimeter problem from November -- you know, the one I mentioned in my Floyd Thursby Day (November 20th) post. It's the problem that the Common Core calls "open-ended," but traditionalists call "ill-posed."

So let's skip to the comments. Of course, SteveH has something to say:

SteveH:

“One-off, open-ended, ill-posed problems that supposedly lead students to apply/transfer prior knowledge to new or novel problems that don’t generalize.”

Little to no transference. Exactly.

No one in-class group problem (open-ended or whatever) offers enough practice to achieve what a proper set of individual homework problem variations provide – unit after proper textbook-scaffolded unit. There is no magic concepts or understanding ideas that will accomplish that. Their magic fairy dust ideas are never presented as a complete longitudinal curriculum from K-8. They offer no examples of success so we are constantly responding to shadows or mere ideas.

SteveH, as usual, assumes that students will actually work on "a proper set of individual homework variations" rather than leave the textbook closed and the paper blank.

SteveH:
I remember trying to help my son prepare for the AMC/12 test related to logarithms. He “understood” what logarithms are all about in concept and for many details. However, what he really needed was to study each and every logarithm problem from previous tests. There is no such thing as a “one-off, open ended” problem that will achieve proper transference to all other problems. There are too many subtle variations that don’t generalize. Full understanding is hidden in all of those homework problem variations.

AMC/12 test takers aren't the typical students sitting in actual math classes. I'm sure that when SteveH showed the first problem variation, his son didn't get the answer completely right the first time. So SteveH told the lad that he was wrong, and his son replied by working harder until he got the correct answer. The teen is motivated to do well because he wants a good score on the AMC/12.

But most students in a Precalculus class won't take the AMC/12. When many students are told that their answer is wrong, they don't work harder to get the correct answer. Instead, they become discouraged, shut down, and leave the rest of the p-set blank. Unfortunately, in real Precalc classes there are more students who shut down at the first sign of difficulty than those who work even harder to get through it.

Indeed, Garelick himself writes:

But imitation is key as one goes up the scale from novice to expert. As anyone knows who has learned a skill through initial imitation of specific techniques, such as drawing, bowling, or learning a dance step—watching something and doing it are two different things. What looks easy often is more complicated than it appears. So too with math. The final accomplishment often does not resemble how one gets there. Like playing a game of football or running a marathon, the building blocks of final academic or creative performance are small, painstaking and deliberate.

I once wrote that in order for students to work on something, it must either be easy, fun, or high status. By "high status," I mean leading to the student being more popular, especially with regards to the attraction of "mates," as in boyfriends/girlfriends. Many of Garelick's examples (artists, dancers, football players) are high status, and so there's a greater tolerance for "painstaking, deliberate" work. On the other hand, math isn't high status, and so students aren't willing to work hard on it. Math must be made easy and fun to make up for the fact that good math students aren't high status (don't attract many girlfriends/boyfriends).

Believe it or not, the most prolific poster in the comment thread isn't SteveH -- it's apparently a new guy, "Stan." Let's see what this Stan has to say:

Stan:

Nice post. I have seen some very clumsy attempts to explain understanding as knowing the connections between facts as if these were not also facts. I can’t imagine any fact that can be stated without connecting two or more things.

Most of the examples, as the one you suggest, where a vague question is posed amount to an implicit claim – I understand perimeters, I know the answer to my new question so if you can’t answer it you don’t understand perimeters. In this https://www.maa.org/sites/default/files/InstructPracGuide_web.pdf on page 13 the new question is whether the student knows that 0 and 1 have different meanings in two parts of the same sentence – in one case they are labels for various identities and in the others they are labels for elements of a set. In both these examples if the notation was explained or better improved it would be much easier to understand and answer the questions.

As it turns out, the link above is intended for college instructors. The example linked above is all about rings. Recall that a ring is a system analogous to the integers -- it has, among, other things, an additive and multiplicative identity. Yes, according to the Common Core Standards, the set of polynomials form a ring, and the additive and multiplicative identity are indeed 0 and 1 respectively.

But in this example, the ring is the set of 2 * 2 matrices. The abstraction is that 0 and 1 are nonetheless the symbols for the identities, even though the multiplicative identity isn't 1 itself but the matrix whose entries are 1, 0, 0, 1. Even though Algebra II students in high school often study matrices, they don't typically use the ring abstraction until college.

Stan:
I absolutely agree. The ill posed question is a very ugly and inaccurate way to measure understanding. It is the antithesis of a mathematical approach. My point was just that yes it will be a crude test of understanding but only someone with little interest in math and an interest in catching people out with mind games would deploy it.
I am a huge fan of aops.com because in part they do an excellent job of offering a progression of challenging questions without playing games. 

Here I assume that "aops.com" refers to https://artofproblemsolving.com/. This is the same site where the late Dr. Kent Merryfield wrote the solutions to Putnam problems. There are sections for the AMC/12 and other high school exams as well.

But once again, AMC/12 and Putnam participants aren't typical of the students sitting in our actual classes. Math teachers "play games" because students who'd tend to leave traditional p-sets blank are more likely to participate in games.

I mention Putnam on the blog in order to inspire students. That doesn't mean I agree with treating all students as if they're future AMC/Putnam participants, and handing them lengthy p-sets or referring them to AOPS. If students are already motivated to excel in math then there's nothing wrong with p-sets and AOPS. But once again, how many students sitting in real high school math classes are so motivated?

Stan:

aops.com is worth looking at. I used it with my son. They are going out of there way to practice well posed challenging problems. While they target those who don’t struggle with math using the right entry point I think anyone would find it worthwhile.

At least Stan is honest here -- he admits that the target audience for AOPS is "those who don't struggle with math," like his (or SteveH's) son. (We'll see whether the traditionalist Stan -- and yes, he's definitely a traditionalist -- will comment more in the future.)

But consider the girl I wrote extensively above in today's post -- the special scholar. Of course, my main problem was my classroom management and interactions with her, and so she was unmotivated to listen to me no matter what. Assume for the sake of argument that I was a strong manager -- would I be able to get her to learn math by referring her to the website of AOPS? Recall that this is a student who had trouble with her 3's Dren Quiz (and what motivated her on the 4's, 5's, and 6's was to avoid further embarrassment after her struggles with 3's).

Before we leave the traditionalists, my attention was drawn to a video that's making the rounds on Facebook. A certain multiplication problem, 35 * 12, is being solved in two different ways. One is the standard algorithm, and the other is to break up 35 and 12 (that is, as 30 + 5 and 10 + 2) and using boxes (as one often uses to multiply polynomials). The person using the standard algorithm is finished so quickly that he/she has time to make coffee before the other is finished. The point obviously being made is that algorithms other than the standard one take too long, so schools should teach only the standard algorithm.

First of all, notice that the comparison isn't an equal one. The person using the alternative method is teaching the viewer how to use the method. The standard algorithm user isn't teaching anything -- that person just assumes that the viewer already knows it. If the standard algorithm were being explained, it would take more time and the race would be a little closer.

Here I assume that the standard algorithm would nonetheless win the race even if both methods were being explicitly taught. But we can replace the box method with another method held in similar disdain by the traditionalists -- the lattice method. Indeed, the lattice method is just like the boxes yet saves a few steps.

Many of my students at the old charter school preferred the lattice method and felt uncomfortable or confused by the standard algorithm. This was especially true among my sixth graders that year. If I took two such students and raced them against each other, the one assigned the lattice method would win, because the one assigned the standard algorithm would leave the paper blank and refuse even to begin.

Now suppose I showed my sixth graders this video, with the standard algorithm winning the race handily. Would that sway them to master the algorithm? Suppose, for example, we were to emphasize "If you master the standard algorithm now, you'll finish your homework faster and have more time to do things, like make coffee." Would that sway them?

This is a tricky one. I suspect that it might work if we had some coffee or another reward right in front of the student, and the students will have more time for the reward if they finish the assignment quickly. But then some students might just leave the p-set blank, so that they have all the time in the world to make coffee. This is more likely to work if the teacher is right in front of the student, of if it's a tutoring situation (like Garelick's beloved Sylvan and Kumon) where the student can't leave the paper blank and escape.

2019 Is an Odd Number to Fawn Nguyen

I usually don't write about Fawn Nguyen in the same post as the traditionalists, but the Queen of the MTBoS is also starting the new year with a new blog post.

http://fawnnguyen.com/2019-is-an-odd-number/

The arrival of 2019 means I have to scroll down even farther to find my age year when I fill out an online form. Ugh… 1985… 1975… 1970… 1967… Here it is… 1965!

Nguyen begins by describing her recent trip to Australia. I can't help but think about another famous MTBoS blogger -- Sarah Carter. Of course, when Sarah went down under, she returned with a husband. Anyway, Nguyen continues:

Around this time, two years ago, I wrote These Twenty Things — the nerve I had to suggest we should do this and that. But, I do wish I had more time to write because recording in this space helps me reflect on what I enjoy most about teaching, which is mainly about what my students take away from a lesson, and perhaps more importantly, what they put into it.

Yes, this means that Nguyen wrote that post during the year I was teaching at the old charter school. But I never acknowledged that post -- at the time, I was reading several other blogs and didn't always check out Nguyen's. Some of her twenty things included:

1. Find a reason to make caramelized onions. You can add it to your favorite pasta sauce or mashed potatoes.
15. Be kind to yourself. Buy that item you didn’t get for Christmas from your favorite person who is now no longer your favorite. If you sleep next to this person, scream, “I hate you!” in the middle of the night like you are dreaming, except you aren’t.
20. Critique the effectiveness of your lesson, not by what answers students give, but by what questions they ask.

Of course, most of my post today is all about evaluating what I should and shouldn't have done two years ago. Apparently, Nguyen is doing the same in her recent post.

She writes about some suggestions for the classroom. Regarding the opening activity:

Begin with a challenging task so everyone has access to it. Fully invite students to work on the problem, individually at first, then in small groups, then with the whole class. When sufficient time has been devoted to this (this can mean 30 minutes or two days, depending on the task and your students), then go do your regular routine, but invite students who finish the regular stuff to continue with the challenging task. I normally see this gets flipped around a lot, that teachers ask students to do the challenging task after they finish their regular work. The problem with this is 1) at least half of the students don’t get to it, and 2) those who get to it don’t care about it simply because the teacher didn’t care enough about it to fully introduce it. It’s not lip service when I introduce each PS with, This is definitely my favorite one!

Let's compare this to what the traditionalists write about problem solving above. They might appreciate that at least the individual work comes first. On the other hand, they might wonder what exactly a "challenging task" is. Based on her "PS" link above, these problems appear to be solvable using both traditional and nonstandard methods, but at least they all seem to be well-posed.

Of course, two years ago I couldn't do any of her PS's even if I wanted, but I could have tried doing some of the Illinois State STEM projects this way. (Here "regular routine" corresponds to the lesson in the traditional Illinois State textbook.) This fits the general Illinois State lesson plan that the STEM project comes before the traditional lesson.

Nguyen now proceeds with some classroom management tips:

Deal with “bad” behaviors in a different (unexpected?) way. I have two recent examples. I was on detention duty, and instead of copying down a selected passage we gave, the student had written a very angry note to another teacher. He had hoped to hide it from me. When I finally got him to produce the note and read it, he started to tear up. I said, “Do you feel better now that you’d written all this down?” He said he was mad and didn’t mean anything by it. I said, “You wrote it, and I read it, and now it’ll go into this garbage can. Done. Sometimes it helps to get it on paper.”

After reading this, I can't help but think about an incident that occurred in October 2016. I didn't mention it in either this year's or last year's Epiphany post, but I did blog about it on the day it actually happened. Right in the middle of my class, some eighth grade girls started writing a smear letter about our English teacher. And yes, involved in this smear was the special scholar, along with her clique.

I'm not sure whether Nguyen's trick would have worked for me that day. After all, these students almost never obeyed my instructions, so "when I finally got him [or her] to produce the note and read it" would equate to never. One excuse the girls would have given me for refusing to hand me the note is that the principal had told them to write it -- after all, the plan all along was to give the principal the note, not the English teacher herself.

In reality, the principal asked them to express a complaint about a teacher in writing -- she never intended them to write it during class time. Indeed, the principal wanted me to stop them from writing it. If I'd been a strong classroom manager, I might have been able to stop them. At the time, my support staff aide was in the classroom, so I probably should have just told her what the girls were doing. The aide likely would have found a way to halt the smear.

Nguyen now proceeds with a book recommendation:

Oh, and there’s a book that you or your school should get. It’s Necessary Conditions by Geoff Krall. I know it says “secondary math,” but that’s some marketing talk, it’s really for any teacher, you!

I've mentioned that most book recommendations I find on the MTBoS aren't the type of math history books that I like to do for our side-along reading. Instead, they're books that are supposed to be helpful to math teachers, like Krall's book above.

If you look at the photo of Krall's book on her blog, you might notice the fine print written on the bottom of the front cover: "Foreword by Fawn Nguyen." Well, that explains why she's so eager to recommend the book!

Hmm, I wonder whether I should read this book for our next side-along reading -- after all, Nguyen wrote the foreword, and I link to her blog all the time, so she's clearly a teacher whose opinion I respect. I usually read cheap books I find at the library book sales (which are at least a decade old), so I'll have to consider whether I wish to purchase a full-priced newer book for our side-along reading.

Conclusion: New Mersenne Prime and Phi Day

I'm continuing to cut and paste from last year's Epiphany post. In last year's post, I wrote about the discovery of the 50th Mersenne prime. I was originally not going to include Mersenne primes in my reblogging, since after all the discovery was made last year.

But guess what -- two weeks ago, a new Mersenne prime was announced: 2^82589933-1:

https://www.mersenne.org/primes/?press=M82589933

The discoverer is Patrick Laroche, an IT professional from Florida. The new prime has over 24 million digits. His computer actually made the discovery on my birthday, but it takes two weeks for a second computer to verify it before it's announced. (The announcement was made on December 21st, the winter solstice and the last day before winter break.)

GIMPS, the computer software responsible for the calculation, is now credited with discovering fully one-third of the known Mersenne primes so far, 17 out of 51.

In January 2017 I played a Numberphile video for my sixth grade class on Mersenne primes, based on an old record-breaker 2^74207281-1. I might as well post that video again:

I showed it to my class in January because that was when the sixth graders reached the unit on prime numbers, but as it turns out, January is a a great month for Mersenne primes. The last four Mersenne primes were discovered in either December or January.

I played this video after a short activity on guessing large primes. As usual, students were talking continuously throughout the activity and video, and so the lesson didn't have as much impact as it would have had in a silence-dominated class. (For once, the special scholar and her clique had nothing to do with the talking, since this was sixth grade, not eighth grade.)

Meanwhile, not only is today Epiphany, but some sources cite today as "Phi Day." Just as Pi Day is March 14th (as in 3.14), since Phi is 1.618033988..., we'd expect Phi Day to be January 61st. But since no month has 61 days, only one digit after the decimal is considered, so Phi Day is January 6th.

[2019 update: I'm reblogging the "Phi Day" portion of this post, but I'm omitting the words "of the Century," which refers to last year, 1/6/18.]

Unfortunately, not only is Phi Day a Sunday, but it's winter break -- many students haven't seen the inside of a classroom in weeks, and they won't return until Monday or Tuesday. But hey -- e is 2.7182818, so we can have an "e Day" on 2/7 -- Thursday, February 7th. So teachers -- Algebra II and above -- should prepare a special celebration for e Day. (Indeed, this year is the earliest date LAUSD students can ever return to class after winter break, which is January 7th. They are guaranteed to have the entire stretch from winter solstice to Epiphany off.)

By the way, here is a new Numberphile video for Phi, posted since last Phi Day:

Returning to Phi, let's look at some Phi Day music. Michael Blake, who set pi to music, also did the same for Phi. Here is "What Phi (the golden ratio) Sounds Like":

I was going to wait until Pi Day for some more coding in Mocha, but since I learned about the special Phi and e Days this year, we might as well do the same for Phi today.

We'll use 38 digits (39 including the initial 1), since this is how many Blake uses in his song:

http://www.haplessgenius.com/mocha/

70 N=1

80 FOR X=1 TO 39

90 READ A

100 SOUND 261-N*(18-A),4

110 NEXT X

120 DATA 1,6,1,8,0,3,3,9,8,8

130 DATA 7,4,9,8,9,4,8,4,8,2

140 DATA 0,4,5,8,6,8,3,4,3,6

150 DATA 5,6,3,8,1,1,7,7,2

Notice that whereas we can avoid the zero problem in pi, zero appears early in Phi, and Blake uses a rest for the zero in his song.

I wrote the above song in 18EDL. Here 0 maps to Degree 18 and 9 maps to Degree 9, one octave higher. Whether it sounds major or minor depends on the preponderance of 3's (18/15 = 6/5, the minor third) or 4's (18/14 = 9/7, the supermajor third) in the DATA lines. Here 3 and 4 appear equally (five times each), but with 3 closer to the start and end, the song sounds more minor.

Thinking back to continued fractions from my Kwanzaa post, it turns out that Phi has a particularly memorable continued fraction:

Phi = (1+sqrt(5))/2 = [1; 1, 1, 1, 1, 1, ...]

And the convergents to Phi are merely the ratios of consecutive Fibonacci numbers:

1/1, 2/1, 3/2, 5/3, 8/5, ....

Because of this, some Fibonacci songs are also great songs to play on a day such as Phi Day. I blogged these back before I started writing music in EDL scales, so let me post EDL versions of these songs:

NEW

70 N=1
80 A=1
90 B=1
100 SOUND 261-N*(12-A),4
110 T=A+B
120 IF T>6 THEN T=T-7
130 A=B
140 B=T
150 GOTO 100

Remember to click the "Sound" box before typing RUN.

Just like the previous versions of the song, this program reduces the Fibonacci numbers mod 7 and then maps the numbers to the scale, except this time it's the simple 12EDL scale. The song itself doesn't use DATA. Instead, the computer actually calculates the Fibonacci numbers. We see how line 110 adds up two numbers, and line 120 performs the reduction mod 7.

To change this to 18EDL, modify the following lines:

100 SOUND 261-N*(18-A),4
120 IF T>9 THEN T=T-10

When I first posted this song over a year ago, I decided to make 1 the tonic rather than 0 and then insert a few rests, as follows:

100 SOUND 261-N*(19-A),4
145 IF (A=0 OR A=6) AND B=A+1 THEN FOR I=1 TO 460:NEXT I:GOTO 110

This was my original rationale for inserting the rests at these locations:

So instead, I want to erase only the 60th note -- the final 0 before it repeats 0-1-1. This avoids the leading tone between Notes 0 and 1. Meanwhile, I also want to avoid the sequence 1-6-7 (which does occur in Fibonacci since 1+6=7). This sequence has a dissonant semidiminished fifth between Notes 1 and 6. Indeed, when I hear this sequence, my ear mistakes 1-6 for a perfect fifth, and then when the true perfect fifth 7 is played, it sounds out of place.

Even though I wasn't referring to 18EDL (or any other EDL scale) at the time, this applies just as well to the 18EDL scale. (If 1 is the tonic at Degree 18, then 7 is Degree 12, and 18/12 = 3/2, which is indeed a perfect fifth.)

Sometimes Phi also appears in microtonal music as well. According to the following video, this is called the "Golden Interval" (as in the Golden Ratio):

The convergents of Phi tell us that the perfect fifth (3/2), the major sixth (5/3), the minor sixth (8/5), the tridecimal neutral sixth (13/8), and so on, are all approximations of the Golden Interval.

We can approximate Golden Intervals in Mocha by putting Fibonacci numbers in the DATA lines, but unfortunately we can use only eight notes instead of ten (with degrees from 8, the sixth Fibonacci number to 233, the thirteenth Fibonacci number). I'm not sure how many Golden Intervals are needed for the song that Izzy Water plays in the video, though.

Let's not forget our other celebration today -- the 51st Mersenne Prime. We wouldn't want to program 24 million digits in a song. So we could just code the first few digits (just as we do for infinite real numbers), or we can just choose a smaller Mersenne prime. For example, the twelfth Mersenne prime 2^127-1 has 39 digits, the same number of digits that Blake uses for Phi:

(Use lines 70-110 from the song for Phi above, not the Fibonacci song.)

120 DATA 1,7,0,1,4,1,1,8,3,4

130 DATA 6,0,4,6,9,2,3,1,7,3

140 DATA 1,6,8,7,3,0,3,7,1,5

150 DATA 8,8,4,1,0,5,7,2,7

I like coding 2^127-1 on Mocha, because this is the highest number she can handle:

PRINT 1.70141183E+38 (works)

PRINT 1.70141184E+38 (gives an ?OV ERROR for overflow)

(That's right -- she. "Mocha" is most likely a girl's name since it ends in "a," and considering that the emulator can play more soprano octaves than bass octaves, the pronoun "she" is appropriate here.)

Notice that this song ends on 7, while both our Phi song and Blake's end on 2. If you prefer a song that ends on 1, try 2^89-1 instead -- it ends in three 1's. The next Mersenne prime 2^521-1 also ends on 1, but the number of digits jumps to 157. Except for the first Mersenne prime 2^2-1 = 3, all Mersenne primes end in either 1 or 7.

But notice that 1 here doesn't refer to the tonic (18) -- instead, 0 is the tonic and 1 is a semitone higher (17). No Mersenne prime ends in 0, so if we want the song to end on 1 as the tonic, we can change 18 to 19 in Line 100 just as we did for Fibonacci.

On the other hand, I like 2^127-1 because 127 is itself a Mersenne prime (2^7-1). I point out that 127 also refers to 12/7, the date the newest prime's discovery. In fact, the following website refers to December 7th as "Mersenne Prime Day":

http://www.albanyconsort.com/mersenne/

Here December 7th was chosen because of the digits "127." It has nothing to do with the discovery of any Mersenne primes (especially considering that this link is so old that only 38 Mersenne primes were known at the time). Indeed, the newest prime is the first to be actually discovered on Mersenne Prime Day.

This concludes my final winter break post. School resumes on Tuesday. On that day we'll begin our second semester with Lesson 8-6 of the U of Chicago text.