7:55 -- This is the start of "second" period (since in this district, "first" period is zero period).
It's the only "Math Studies" class of the day. Recall that "Math Studies" is part of the IB program. It's a very small class with only ten students (including the senior TA), mostly juniors.
The students recently took a test, and now they are doing test corrections for points. Two guys in the class earned F's on the test, and I do try to help them with their corrections. Fortunately, both of them are sitting next to the girl who earned the highest score in the class -- 102%. She willingly helps the other two guys with their corrections.
What exactly are the contents of this test? Well, I wrote extensively about the IB Math Studies class around this time last year. Let me reblog some of what I wrote last year:
I learn that the IB exam consists of seven different topics:
1. Numbers and Algebra
2. Descriptive Statistics
3. Logic, Sets, and Probability
4. Statistical Applications
5. Geometry and Trigonometry
6. Mathematical Models
7. Introduction to Differential Calculus
Let's look at Topic 5 in more detail -- not only because this is a Geometry blog, but also because this is what the second period students are currently reviewing:
5.1 Equation of lines
5.2 Trigonometric ratios
5.3 Sine and cosine rule; area of a triangle
5.4 Three-dimensional solids
5.5 Volume and surface area of three-dimensional solids
So we see that just as with the SAT, the IB gives Geometry short shrift. Subtopic 5.1 is really just Algebra in disguise. Subtopics 5.2 and 5.3 go beyond the trig we learn in Chapter 14 of the U of Chicago text. Subtopics 5.4 and 5.5 are equivalent to Chapters 8-10 -- I include the area chapters since the volume and surface area formulas are derived from area formulas. The rest of the text doesn't appear on the IB exam at all.
We notice that since this is the International Baccalaureate exam, many of the terms used on the exam are Commonwealth rather than American. The word "gradient," for slope, is interesting. In Multivariable Calculus (a college-level class, the next step beyond Calc BC), we learn about a generalization of the derivative called the "gradient." We now see that "gradient" is the international word for "slope" even in Algebra problems.
The equation of a line is y = mx + c, not y = mx + b. (And I still don't know what the letter m has to do with slope!) Notice that y = mx + c is still called "slope-intercept form," not "gradient-intercept." I guess since c appears in the slope-intercept form, we have to use d in the standard form of a line instead, so it's ax + by + d = 0.
Other international terms include "sine rule" and "cosine rule" -- of course, American texts would call these "Law of Sines" and "Law of Cosines."
Returning to 2019, yes, the students are currently working on Topic 5 again this year. I help one guy (one of the two who failed) on a simple right triangle trig problem like those of Lesson 14-3 -- all we need to solve the problem is the tangent ratio. But on the test, he'd tried to use sine instead. I didn't realize it at the time, but I suspect now that he was trying to use the "sine rule" (Law of Sines), even though it was a right triangle. In hindsight, I wonder whether the teacher had expected him to use the sine rule anyway, since the IB stresses the sine and cosine rules.
8:45 -- Second period leaves and third period arrives. All remaining classes are Honors Algebra II.
In all the Algebra II classes, the students are taking their test today. No, these students aren't currently working on trig (as all the classes from Geometry to IB Math Studies seem to be now). Instead, the topic is simplifying rational expressions.
This teacher actually uses cardboard dividers to prevent cheating. As a young student, I haven't seen cardboard dividers since third grade, so I'm surprised to see them in high school. (And even in third grade, I believe we only used it for state standardized testing, the CTBS.) The teacher also has the students place all backpacks and phones at the front whiteboard.
Third period is the only period in which mention that Pi Day is coming. I suppose that it's close enough to Pi Day to start mentioning it -- and besides, the way my subbing has been going lately, I might not sub in another math class until well after the holiday. I write about Pi Day on the board, but it's hard for me to talk about it since I must make sure there's enough time to take the test -- many students don't finish until class is just about over.
In addition, I must tell the students about the homework. On Monday, there's a math Performance Task coming up. (OK, so the English Performance Task in this district is before President's Day while the math PT is afterward.) The students should refer to quadratic equations in their notes -- either in a notebook or in Google Classroom -- to prepare for it. They must also turn in a completed homework packet for the current Chapter 7.
9:40 -- Third period leaves. It is now time for tutorial.
Most of the math help I give today is during tutorial (since I can't help during the test). Many of the students are confused about asymptotes, and so I give them the following examples:
y = 6x/(x^2 + 1) has a horizontal asymptote at y = 0, the x-axis.
y = 6x^2/(x^2 + 1) has a horizontal asymptote at y = 6.
y = 6x^3/(x^2 + 1) has a slant asymptote at y = 6x.
y = 6x^4/(x^2 + 1) has no asymptote.
In hindsight, I should have made the denominators 2x^2 + 1 instead of x^2 + 1. Then the students can clearly see the division, especially for y = 6x^2/(2x^2 + 1), where the asymptote is found by dividing the leading coefficients -- y = 6/2 = 3.
Later on, I also realize that I could have helped the students more with stating restrictions on the variables to prevent any denominator from being zero. Notice that in a division of fractions problem such as (a/b) / (c/d), a can be zero, but none of b, c, d can be zero. In general, any expression that ever appears in the denominator at any point in the problem must be nonzero, including both the denominator of the divisor (even though it's about to be flipped to the numerator), as well as factors that are about to cancel (leading to holes in the graph).
10:25 -- Tutorial ends and the students leave for snack.
10:45 -- Fourth period arrives. I end up naming them the second best class of the day. (The only behavior to keep track of is silence during the test.)
11:35 -- Fourth period leaves and fifth period arrives. I end up naming them the best class of the day.
12:30 -- Fifth period leaves for lunch.
1:15 -- Sixth period arrives.
This is the only class during which I mention something I wrote about back in my Epiphany post -- the importance of rational expressions to passing college-level math. It was traditionalist Barry Garelick who pointed out that passage of the college placement exam correlates with success on a single item on that test -- and it's on simplifying rational expressions.
Here's what I wrote about that problem back in January (quoting Garelick):
On a placement test for entering freshmen at California State University, a single item on the exam correlated extremely well with passing the exam and subsequent success in non-remedial college math. The problem was to simplify the following expression. (Multiple choice test):
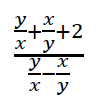
The argument here, of course, is that this is the sort of problem Garelick wants to see more of in high school math. Even though simplifying rational expressions appears in Common Core Standards, it's probably not emphasized as much as the traditionalists desire. The (+) sign in the standards implies that this will likely be delayed to Precalculus, while the traditionalists would like to see it in Algebra II.
Today in class, I decide to write Garelick's problem on the board. As the students slowly complete the test, I point to this question on the board and tell them that it's a college placement question -- and that if they know how to solve it, they'll probably succeed in college math.
2:05 -- Sixth period ends, and this teacher doesn't have a seventh period, so my day is done.
But I continue to discuss the problem with some students who are slow to leave (since they just barely finish the test before the end of class). Most of the students are sophomores which is typical for an honors Algebra II class, since sophomores in this class are generally honors students who might even be part of the IB program. (Traditionalist SteveH regularly includes IB as a program which he greatly respects.)
As it turns out, one girl in the sixth period class is only a freshman. As I show her Garelick's problem, I inform her that I myself took Algebra II as a young freshman. She replies that she's always enjoyed learning math.
Two other girls stay behind a few minutes since their seventh period class is track practice -- they're sprinters -- and practice always begins a few minutes late anyway. They attempt to solve the Garelick problem -- though I must help them on a few steps, they eventually solve it. They were pleasantly surprised to find out that they've solved the college-bound problem.
Let's look at a focus resolution:
4. Begin the lesson quickly instead of having lengthy warm-ups.
This is the only resolution that's especially relevant today -- begin the test quickly instead of fooling around with other business. And this is exactly what I do today -- I have the students place their backpacks at the front of the room as they arrive, and so I go straight into attendance and the test. I actually could have skipped attendance and take the names directly off of the tests (since unlike a regular assignment, the students won't just leave the test blank). But this would have been awkward since some sophomore students needed to leave after the test to finish their IB essay.
Indeed, I wrote the following paragraph last year:
Back when I was a student teacher, my school had an IB program -- and indeed, I taught an Algebra I class for IB freshmen. Presumably, some IB freshmen also took Geometry, but I only taught the Algebra I class. But if I'm not mistaken, the IB program at this school no longer exists -- it was replaced by an AP-based magnet.
And there were actually a handful of sophomores in that Algebra I class -- and I remember they were telling me about the IB essay.
Regarding attendance, there are also several students out on a field trip. I believe that it's a special field trip for certain IB students -- and that they won't return until Sunday night. (I never find out where exactly they went on the field trip.)
Speaking of Barry Garelick, I see a new post visible on his website. It is dated March 9th -- even though I can read the post tonight, March 8th. Since the post is dated Saturday (which timezone?) and no one has commented on it yet, I'll save a discussion of Garelick's latest post for Monday. (Then again, I kept mentioning Garelick and SteveH in today's post anyway, even though it's not officially a traditionalists' post.)
This is what I wrote last year about today's lesson:
Section 12-6 of the U of Chicago text covers the Fundamental Theorem of Similarity. As its name implies, it is the most important theorem related to dilations and similarity. Here is how this theorem is stated in the U of Chicago:
Fundamental Theorem of Similarity (U of Chicago):
If G ~ G' and k is the ratio of similitude, then
(a) Perimeter(G') = k * Perimeter(G) or ...
(b) Area(G') = k^2 * Area(G) or ...
(c) Volume(G') = k^3 * Volume(G) or ...
Notice how I had to rewrite this theorem so that it fits into ASCII. Here the * and ^ symbols denote multiplication and exponentiation, respectively -- these symbols should be recognizable as they appear on TI graphing calculators. The "or ..." sections refer to the text rewriting each equation as a ratio, so that the ratio of the perimeters is k, the ratio of the areas is k^2, and so on, but that is rather awkward to write in ASCII.
David Joyce describes this theorem in his criticism of the Prentice-Hall text:
The proofs are omitted for the theorems which say similar plane figures have areas in duplicate ratios, and similar solid figures have areas in duplicate ratios and volumes in triplicate rations. At least there should be a proof that similar triangles have areas in duplicate ratios; that's easy since the areas of triangles are already known.
Here is the U of Chicago proof:
(a) Perimeter is just the sum of the lengths. Suppose lengths a, b, c, d, e, ...make up the perimeter of G. Then lengths ka, kb, kc, kd, ke, ...make up the perimeter of G'.
Perimeter(G') = ka + kb + kc + kd + ke + ...
= k(a + b + c + d + e + ...)
= k * Perimeter(G)
(b) Let A = the area of G. Then you could think of the area of G as the sum of areas of A unit squares. Then the area of G' is the sum of areas of A squares k units on a side. Since each square in G' has area k^2,
Area of G' = A * k^2 = k^2 * Area of G.
(c) The argument is identical (except with unit cubes). QED
As I mentioned earlier this week, I'm no longer posting old worksheets that mention the Hung-Hsi Wu proof. Thus I'm rearranging last year's worksheets.
Last year's second worksheet is now the first worksheet, since it mentions the U of Chicago version of the Fundamental Theorem of Similarity.
Today is an activity day. I decided to keep the activity that I posted last year for Lesson 12-5 (that I dropped from the Thursday lesson this year). There's no point in using the Lesson 12-6 Exploration question from the U of Chicago text since it asks students to take the scale model from Lesson 12-5 (in other words, we can't avoid 12-5 anyway) and then weigh it (which students probably can't do since most math classrooms don't even have scales for weighing objects).


No comments:
Post a Comment